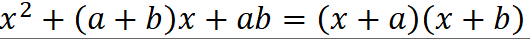数与式

• ​实数

  • ​定义：有理数和无理数统称为实数

  • ​分类

    • ​有理数：整数与分数

    • ​无理数：开方开不尽的数、与 $π$ 有关的数、无限不循环小数

  • ​实数的运算

    • ​法则：加、减、乘、除、乘方、开方

    • ​运算定律：交换律、结合律、分配律

  • ​相关概念

    • ​数轴(比较大小)、相反数、倒数(负倒数)科学记数法

    • ​有效数字、平方根与算术平方根、立方根、非负式子

• ​整式

  • ​分类

    • ​单项式：系数与次数

    • ​多项式：次数与项数

  • ​加减法则(加减法、去括号(添括号)法则、合并同类项整式

  • ​幂的运算：同底数幂相乘底数不变指数相加，同底数幂相除底数不变指数相减，幂的乘方底数不变指数相乘

  • ​乘法运算

    • ​单项式×单项式；单项式×多项式;多项式×多项

    • ​单项式÷单项式；多项式÷单项式

  • ​混合运算：先乘方开方，再乘除，最后算加减；同级运算自左至右顺序计算;括号优先

  • ​乘法公式

    • ​完全平方公式  

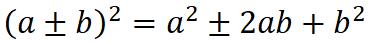
    • ​平方差公式：

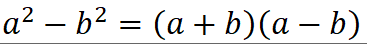
• ​分式

  • ​分式

    • ​分式的定义:分母中含可变字母

    • ​分式有意义的条件:分母不为零

    • ​分式值为零的条件:分子为零，分母不为零

  • ​分式的性质：，

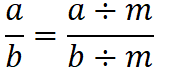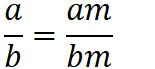
  • 分式的运算

    • ​通分、约分，加减乘除

    • ​化简求值

      • ​先化简再求值

      • 整体带入求值

• 二次根式

  • ​定义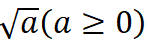：叫二次根式

  • ​二次根式的运算

    • ​加减法：先化最简，再合并同类二次根式

    • 乘除法：

      ​

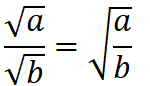
• 因式分解

  • ​提公因式

  • ​公式法

    • ​平方差公式

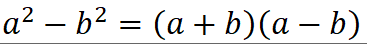
    • ​  完全平方公式

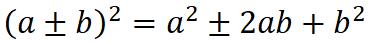
  • ​十字相乘法：