认识三角形_副本
基本概念
由不在同一直线上的三条线段,首尾顺次相接所组成的图形
组成要素、必备知识
符号表示
符号表示
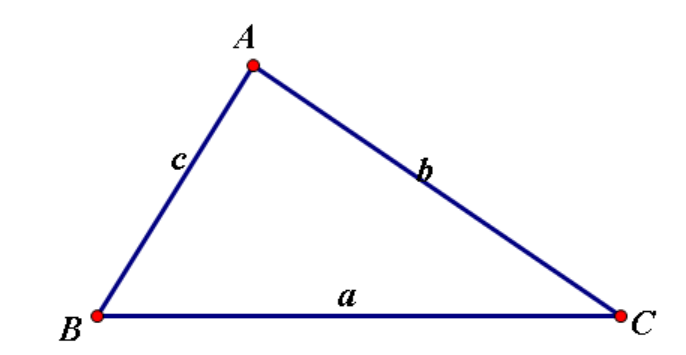 记作
记作
内角和
三个内角的和为
外角
图例
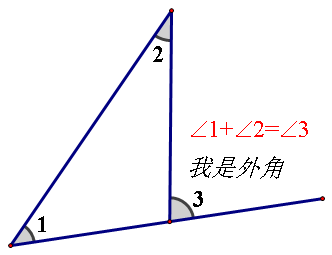
定义
三角形的一条边与另一条边的延长线组成的角
性质
三角形的一个外角等于与它不相邻两个内角之和
三线&三心
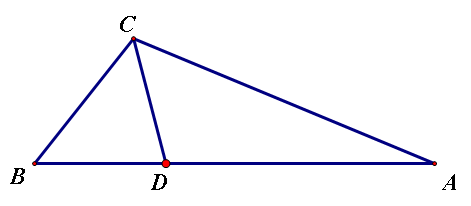
中线
三角形中,连接一个顶点与它对边中点的线段
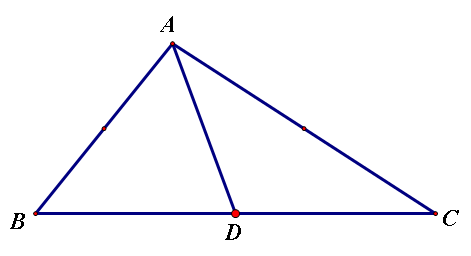
性质
等分三角形面积
重心💗
三角形三条中线交于一点,这点称为
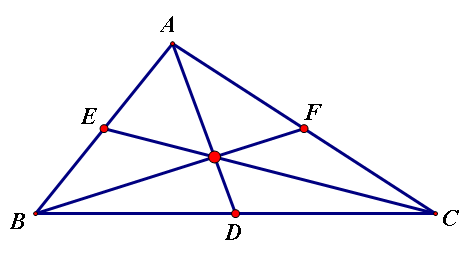
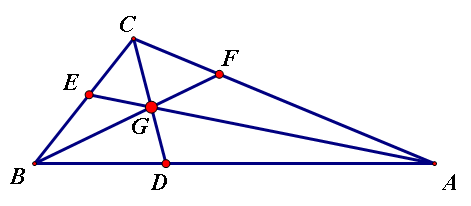
角平分线
从,一个角的顶点引出的能把这个角分成两个完全相同的角,的射线
内💗
三角形三条角平分线交点一点,这点成为
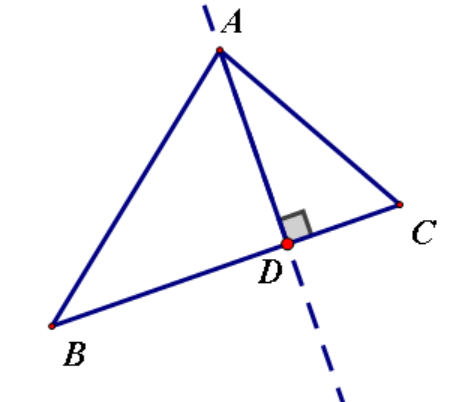
高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段
垂💗
三角形三条高的交点

分类
角
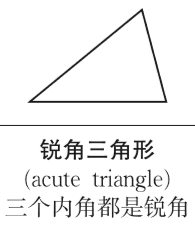
锐角三角形
直角三角形
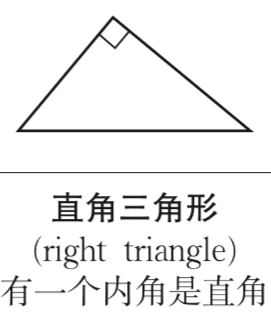
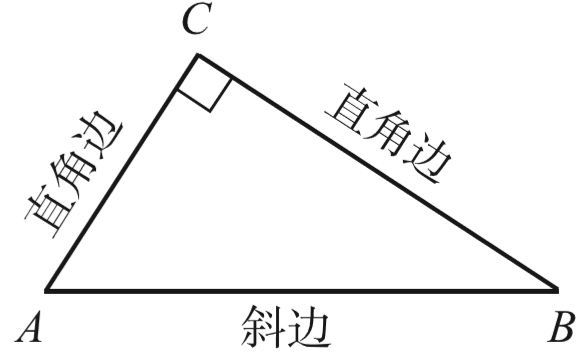
符号
直角三角形两个锐角的性质
直角三角形两个锐角互余
钝角三角形
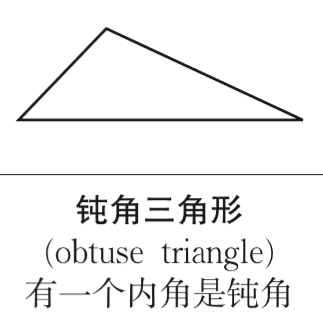
注意
仅一个锐角不能判定三角形形状
应以最大的内角为准
边
不等边三角形
三边都不相等
等腰三角形
只有两边相等
等腰三角形

性质
两腰相等、两底角相等
三边都相等
等边三角形 正三角形
三边相等、三个内角都为
三边关系
性质
性质1
两边之和大于第三边
性质2
两边之差小于第三边
应用
已知两边的长度求第三边的取值范围
判定
方法1
将较短的两边相加,与第三边比较
方法2
将最长边与最短边相减,与第三边比较