-
猴博士_概率论与数理统计课程笔记
概率论
事件的概率
无放回
有放回
二维图形面积(权重相等)概率计算
需要坐标系作图
条件概率
A 已经发生时,B发生的概率
全概率公式
一维随机变量
已知累积分布函数求解概率密度函数或者相反
已知CDF或者PSD中的一种,求解P
CDF或者PDF函数中含有未知数,求解未知数
求分布列
离散随机变量的所有取值和对应概率用表列出来
含有未知数的分布列,求未知数
一维随机变量的函数
已知X的分布列和y=f(x),求Y的分布列
已知
写出
将 替换
中的 ,得到
判断 中是否有负号
若无
若有:
检查确认y的区间
已知 ,求
写出
将 替换
中的 ,得到
令
f Y = ( ? y ) ′ ⋅ f X ( ? y ) f_Y = (?y)'\cdot f_X(?y)
判断
? y ?y 若无:
f Y ( y ) = f Y f_Y(y) = f_Y
若有:
f Y ( y ) = − f Y f_Y(y) = -f_Y
常见的5种分布
均匀分布
U [ a , b ] U[a,b]
U [ a , b ] ( x ) = { 1 b − a , a < x < b 0 , o t h e r U[a,b](x) = \begin{cases} \frac{1}{b-a}, a \lt x\lt b \\ 0,other \end{cases}
泊松分布
P ( X = x ) = λ x x ! e − λ P(X=x) =\frac{\lambda^x}{x!}e^{-\lambda}
二项分布
B [ n , p ] B[n,p]
P ( X = x ) = C n x p x ( 1 − p ) n − x P(X=x)= C_{n}^{x}p^x(1-p)^{n-x}
指数分布
E ( λ ) E(\lambda)
f ( x ) = { λ e − λ x , x > 0 0 , x ≤ 0 f(x) = \begin{cases} \lambda e^{-\lambda x},x >0\\ 0,x\le 0 \end{cases}
正态分布
N ( μ , σ 2 ) N(\mu,\sigma^2) N ( μ , σ 2 ) ∼ f ( x ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) N(\mu,\sigma^2) \sim f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(- \frac{(x-\mu)^2}{2\sigma^2}\right)
N ( 0 , 1 ) , Φ ( u ) = ∫ − ∞ u f ( x ) d x N(0,1),\Phi(u) = \int_{-\infty}^{u}f(x)dx
P ( a < X < b ) = Φ ( b − μ σ ) − Φ ( a − μ σ ) P ( X < a ) = Φ ( a − μ σ ) P ( X > b ) = 1 − Φ ( b − μ σ ) P(a \lt X\lt b) = \Phi(\frac{b-\mu}{\sigma}) - \Phi(\frac{a-\mu}{\sigma})\\ P(X\lt a) = \Phi(\frac{a-\mu}{\sigma}) \\ P(X\gt b) = 1 - \Phi(\frac{b-\mu}{\sigma})
正态分布的图像
N ( μ , σ 2 ) N(\mu ,\sigma^2) 图像
x = μ x = \mu
曲线与
x x
σ \sigma μ \mu
离散型二维变量和连续性二维变量(上)
已知二维离散型分布列,求概率/分布列
已知二维离散型分布列,判断其独立性
独立性判断,对于任意的
x i , y i x_i,y_i P ( X = x i , Y = y i ) = P ( X = x i ) P ( Y = y i ) P(X=x_i,Y=y_i) = P(X=x_i)P(Y=y_i) X X Y Y
已知二维连续联合分布函数CDF,求二维连续联合概率密度函数PSD
f ( x , y ) = = ∂ 2 F ( x , y ) ∂ x ∂ y f(x,y) = = \frac{\partial ^2 F(x,y)}{\partial x \partial y}
已知二维连续联合概率密度函数PSD,求二维连续联合分布函数CDF
首先在
f ( x , y ) f(x,y) x x y y
计算
∫ g 1 ( x ) x d u ∫ h 1 ( u ) y f ( u , v ) d v \int_{g_1(x)}^{x}du \int_{h_1(u)}^y f(u,v)dv ( 1 ) (1)
g 1 ( x ) g_1(x)
h 1 ( u ) h_1(u) y y x x u u
f ( u , v ) f(u,v) f ( x , y ) f(x,y) x x u u y y v v
将
x = g 2 ( y ) , y = h 2 ( x ) x = g_2(y),y= h_2(x) ( 1 值) (1) ( 2 ) , ( 3 ) (2),(3)
画出
f ( x , y ) f(x,y)
A的右侧区域记作B
A的上侧区域记作C
A的右上方区域记作D
F ( x , y ) = { ( 1 ) , A ( 2 ) , B ( 3 ) , C 1 , D 0 , o t h e r F(x,y) = \begin{cases} (1), A\\ (2),B\\ (3),C\\ 1,D\\ 0, other \end{cases}
已知
F ( x , y ) F(x,y) P P P ( X ≤ x 0 , Y ≤ y 0 ) = F ( x 0 , y 0 ) P(X\le x_0,Y\le y_0) = F(x_0,y_0)
已知
f ( x , y ) f(x,y) P P P ( X ≤ x 0 , Y ≤ y 0 ) = ∫ − ∞ x 0 d x ∫ − ∞ y 0 f ( x , y ) d y P(X\le x_0,Y\le y_0) = \int_{-\infty}^{x_0}dx\int_{-\infty}^{y_0}f(x,y)dy
求
F ( x , y ) , f ( x , y ) F(x,y),f(x,y)
F ( + ∞ , + ∞ ) = 1 F ( − ∞ , − ∞ ) = 0 F ( x , − ∞ ) = 0 F ( − ∞ , y ) = 0 ∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d x d y = 1 F(+\infty,+\infty) = 1\\ F(-\infty,-\infty) = 0\\ F(x,-\infty) = 0\\ F(-\infty,y) = 0\\ \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}f(x,y)dxdy = 1
求均匀分布的密度函数和概率
离散型二维变量和连续性二维变量(下)
已知联合分布CDF,求边缘分布函数
F X ( x ) = F ( x , + ∞ ) F Y ( y ) = F ( + ∞ , y ) F_X(x) = F(x,+\infty) \\ F_Y(y) = F(+\infty,y
F X ( x ) = F ( x , + ∞ ) F Y ( y ) = F ( + ∞ , y ) F_X(x) = F(x,+\infty) \\ F_Y(y) = F(+\infty,y)
已知联合分布密度函数,求边缘分布密度函数
将
f ( x , y ) f(x,y)
表示出该区域的左边界右边界上边界下边界分别为
x = g 1 ( x ) , x = g 2 ( x ) , y = h 1 ( x ) , y = h 2 ( x ) x=g_1(x),x=g_2(x),y=h_1(x),y=h_2(x)
f X ( x ) = ∫ h 2 ( x ) h 2 ( x ) f ( x , y ) d y f Y ( y ) = ∫ g 1 ( y ) g 2 ( y ) f ( x , y ) d x f_X(x) = \int_{h_2(x)}^{h_2(x)}f(x,y)dy \\ f_Y(y) = \int_{g_1(y)}^{g_2(y)}f(x,y)dx
判断连续型二维变量的独立性
F ( x , y ) = F X ( x ) F Y ( y ) f ( x , y ) = f X ( x ) f Y ( y ) F(x,y) = F_X(x)F_Y(y) \\ f(x,y) = f_X(x)f_Y(y)
已知
f ( x , y ) , Z = F ( X , Y ) f(x,y),Z=F(X,Y f ( x , y ) , Z = X + Y f(x,y),Z=X+Y f Z ( z ) f_Z(z) f ( x , y ) f(x,y f ( x , y ) , Z = F ( X , Y ) f(x,y),Z=F(X,Y) f Z ( z ) = ∫ − ∞ + ∞ f ( x , z − x ) d x f_Z(z) = \int_{-\infty}^{+\infty}f(x,z-x)dx
已知
f ( x , y ) , Z = X Y f(x,y),Z = \frac{X}{Y} f Z ( z ) f_Z(z) f Z ( z ) = ∫ − ∞ + ∞ f ( y z , y ) ∣ y ∣ d y f_Z(z) = \int_{-\infty}^{+\infty}f(yz,y)|y|dy
( x , y ) , Z = max ( X , Y ) f(x,y),Z=\max(X,Y)已知 f Z ( z ) f_Z(z) f Z ( z ) = F X ( z ) F Y ( z ) f_Z(z) = F_X(z)F_Y(z)
( x , y ) , Z = max ( X , Y ) f(x,y),Z=\max(X,Y)已知 f Z ( z ) f_Z(z) f Z ( z ) = ( 1 − F X ( z ) ) ( 1 − F Y ( z ) ) f_Z(z) = (1-F_X(z))(1-F_Y(z))
随机变量的数字特征(上)
求离散型变量的期望
E ( X ) = ∑ i x i p I E(X) = \sum_{i} x_i p_I E ( X ) = ∑ i x i p i E(X) = \sum_{i} x_i p_
求连续型的期望
E ( X ) = ∫ − ∞ + ∞ x f ( x ) d x E(X) = \int_{-\infty}^{+\infty}xf(x)dx
已知
Y = g ( x ) Y = g(x) E ( Y ) E(Y) 离散型
E ( X ) = ∑ i g ( x i ) p i E(X)=\sum_i g(x_i)p_i
连续型
E ( X ) = ∫ − ∞ + ∞ g ( x ) f ( x ) d x E(X) = \int_{-\infty}^{+\infty}g(x)f(x)dx
求方差
离散型
D ( X ) = ∑ i [ x i − E ( x ) ] 2 p i D(X) = \sum_i [x_i - E(x)]^2p_i
连续型
D ( X ) = E ( X 2 ) − E 2 ( X ) D(X) = E(X^2) - E^2(X)
利用期望和方差性质做复杂运算
期望的性质
E ( C ) = C E ( C X ) = C E ( X ) E ( X ± Y ) = E ( X ) ± E ( Y ) E ( X Y ) = E ( X ) E ( Y ) E(C)= C\\ E(CX) = CE(X) \\ E(X\pm Y) = E(X)\pm E(Y)\\ E(XY) = E(X)E(Y
最后一条需要XY相互独立
方差的性质
D ( C ) = 0 D ( C X ) = C 2 D ( X ) D ( X ± Y ) = D ( X ) + D ( Y ) D(C) = 0 \\ D(CX) = C^2 D(X)\\ D(X\pm Y) = D(X) + D(Y) 最后一条需要XY相互独立
练习期望和方差
D ( X ) = E ( X 2 ) − E 2 ( X ) D(X) = E(X^2) - E^2(X)
期望、方差与各种分布的综合题
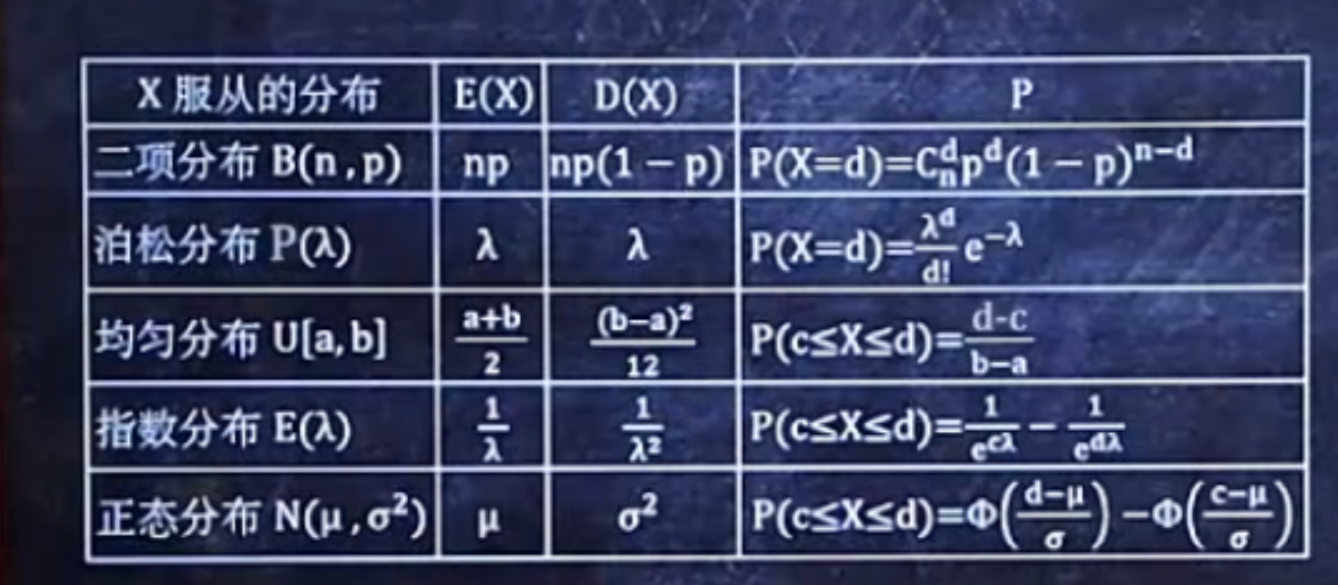
常用5种分布的期望和方差
随机变量的数字特征(下)与中心极限定理
C o v , ρ x y , D {\rm{Cov}},\rho_{xy},D 协方差相关公式
C o v ( X , Y ) = E ( X Y ) − E ( X ) ⋅ E ( Y ) C o v ( X , X ) = D ( X ) C o v ( X , Y ) = 0 ( ∗ ) C o v ( X , Y ) = ρ X Y D ( X ) D ( Y ) C o v ( a X + b , c Y + d ) = a c C o v ( X , Y ) C o v ( X 1 ± X 2 , Y ) = C o v ( X 1 , Y ) ± C o v ( X 2 , Y ) C o v ( X , Y 1 ± Y 2 ) = C o v ( X , Y 1 ) ± C o v ( X , Y 2 ) {\rm{Cov}}(X,Y) = E(XY) - E(X)\cdot E(Y)\\ {\rm{Cov}}(X,X) = D(X)\\ {\rm{Cov}}(X,Y) = 0 (*)\\ {\rm{Cov}}(X,Y) = \rho_{XY}\sqrt{D(X)}\sqrt{D(Y)} \\ {\rm{Cov}}(aX+b,cY+d) = ac {\rm{Cov}}(X,Y) \\ {\rm{Cov}}(X_1 \pm X_2,Y) = {\rm{Cov}}(X_1,Y) \pm {\rm{Cov}}(X_2,Y) \\ {\rm{Cov}}(X,Y_1\pm Y_2) = {\rm{Cov}}(X,Y_1) \pm {\rm{Cov}}(X,Y_2)
(*) 要求XY相互独立
相关系数相关公式
ρ X Y = C o v ( X , Y ) D ( X ) D ( Y ) ρ X Y = 0 ( ∗ ) \rho_{XY} = \frac{{\rm{Cov}}(X,Y)}{\sqrt{D(X)D(Y)}} \\ \rho_{XY} = 0 (*) (*)要求XY相互独立
方差相关公式
D ( X ± Y ) = D ( X ) + D ( Y ) ± 2 C o v ( X , Y ) D(X\pm Y) = D(X) + D(Y) \pm 2{\rm{Cov}}(X,Y)
利用切比雪夫不等式求概率
P [ ∣ X − E ( X ) ∣ ≥ ϵ ] ≤ D ( X ) ϵ 2 P[|X-E(X)|\ge \epsilon ] \le \frac{D(X)}{\epsilon^2}
-
中心极限定理
设随机变量
x 1 , x 2 , . . . , x n x_1,x_2,...,x_n μ \mu σ 2 \sigma^2 x ˉ = ∑ x i n \bar{x}=\frac{\sum x_i}{n} n n μ \mu σ 2 n \frac{\sigma^2}{n} n → ∞ n→\infty x ˉ → N ( μ , σ 2 n ) \bar{x} \to N(\mu,\frac{\sigma^2}{n})
数理统计(本科的时候没学,故略过)
数理统计基础
求离散型变量的期望
E ( X ) = ∑ i x i p I E(X) = \sum_{i} x_i p_I E ( X ) = ∑ i x i p i E(X) = \sum_{i} x_i p_
求连续型的期望
E ( X ) = ∫ − ∞ + ∞ x f ( x ) d x E(X) = \int_{-\infty}^{+\infty}xf(x)dx
已知
Y = g ( x ) Y = g(x) E ( Y ) E(Y) 离散型
E ( X ) = ∑ i g ( x i ) p i E(X)=\sum_i g(x_i)p_i
连续型
E ( X ) = ∫ − ∞ + ∞ g ( x ) f ( x ) d x E(X) = \int_{-\infty}^{+\infty}g(x)f(x)dx
求方差
离散型
D ( X ) = ∑ i [ x i − E ( x ) ] 2 p i D(X) = \sum_i [x_i - E(x)]^2p_i
连续型
D ( X ) = E ( X 2 ) − E 2 ( X ) D(X) = E(X^2) - E^2(X)
利用期望和方差性质做复杂运算
期望的性质
E ( C ) = C E ( C X ) = C E ( X ) E ( X ± Y ) = E ( X ) ± E ( Y ) E ( X Y ) = E ( X ) E ( Y ) E(C)= C\\ E(CX) = CE(X) \\ E(X\pm Y) = E(X)\pm E(Y)\\ E(XY) = E(X)E(Y
最后一条需要XY相互独立
方差的性质
D ( C ) = 0 D ( C X ) = C 2 D ( X ) D ( X ± Y ) = D ( X ) + D ( Y ) D(C) = 0 \\ D(CX) = C^2 D(X)\\ D(X\pm Y) = D(X) + D(Y) 最后一条需要XY相互独立
练习期望和方差
D ( X ) = E ( X 2 ) − E 2 ( X ) D(X) = E(X^2) - E^2(X)
期望、方差与各种分布的综合题
常用5种分布的期望和方差
矩估计
求某一未知参数的矩估计(用期望)
设一大批产品的不合格率为P,每次从中抽取10件进行检验,用
x i x_i i i x 1 , x 2 , . . . , x n x_1 ,x_2,...,x_n B ( 10 , P ) B(10,P) 写出期望与待求位置数的关系
E ( X ) = n P = 10 P E(X) = nP = 10P E ( X ) = n P = 10 P E(X) = nP = 10P ( X ) = 10 P E(X) = 10P E ( X ) = n P = 10 P E(X) = nP = 10P
整理上式得到
P = E ( X ) 10 P = \frac{E(X)}{10}
根据样本,算出得到实际的期望
E ( X ) = ∑ i x i n E(X) = \frac{\sum_i{x_i}}{n}
将实际期望代入求未知数
P ^ \hat{P}
求某两个未知参数的矩估计(用期望+方差)
设总体X在[a,b]上服从均匀分布,a和b均未知,
x i x_i 写出期望和方差与待求未知数的关系
E ( X ) = ( a + b ) 2 D ( X ) = ( b − a ) 2 12 E(X) = \frac{(a+b)}{2} \\ D(X) = \frac{(b-a)^2}{12}
a = E ( X ) − 3 D ( X ) E ( X ) b = E ( X ) + 3 D ( X ) E ( X ) a = E(X) - 3\frac{D(X)}{E(X)} \\ b = E(X) + 3\frac{D(X)}{
根据样本,算出得到实际的期望
E ( X ) = ∑ i x i n E(X) = \frac{\sum_i{x_i}}{n} D ( X ) = E ( X 2 ) − E 2 ( X ) D(X) = E(X^2) - E^2(X)
将实际期望和实际方差代入求未知数
a ^ , b ^ \hat{a},\hat{b}
最大似然估计量
求某离散型参数的最大似然估计量
求出某连续型参数的最大似然估计量
区间估计
假设检验
判断单项参数与某数值的关系
判断两项参数间的关系
对于成对数据的检验
P值检验
方差分析
一元线性回归
Y = a ^ + b ^ x S x y = ∑ i ( x i y i ) − ( ∑ i x i ) ( ∑ i y i ) n S x x = ∑ i x i 2 − ( ∑ i x i ) 2 n b ^ = S x y S x x a ^ = ∑ i y i n − ∑ i x i n b ^ Y = \hat{a} + \hat{b}x \\ S_{xy} = \sum_{i}(x_iy_i)- \frac{(\sum_i x_i)(\sum_{i} y_i)}{n}\\ S_{xx} = \sum_{i} x_i^2 - \frac{(\sum_{i}x_i)^2}{n}\\ \hat{b} = \frac{S_{xy}}{S_{xx}} \\ \hat{a} = \frac{\sum_{i}y_i}{n} - \frac{\sum_{i}x_i}{n}\hat{b}
求一元线性回归模型系数
对一元线性回归模型的方差进行估计
在一元线性回归模型中检验回归效果显著性
在一元线性回归模型中求系数b的置信区间
Y约为x的指数函数时,求Y关于x的回归方程