电子自旋和全同粒子
自旋算符
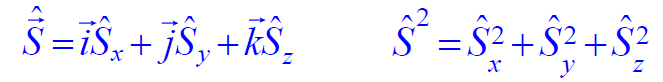
对易关系
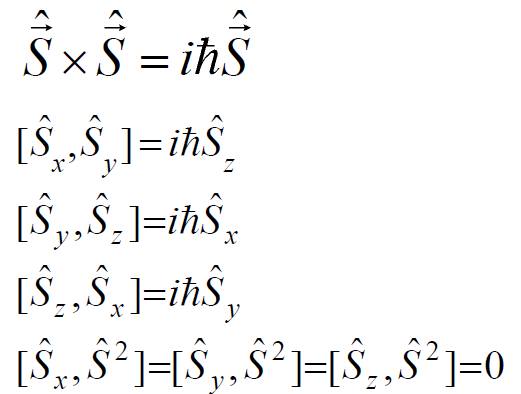
S=1/2时
pauli算符
和 概括了 的全部代数性质
的分量之间满足反对易关系
自旋算符的矩阵形式——pauli矩阵
电子自旋态
电子自旋磁矩
电子自旋磁矩等于一个玻尔磁子
电子自旋磁矩算符
轨道磁矩算符:
与外磁场的作用能
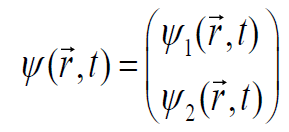 规定第一行对应 ,第二行对应
规定第一行对应 ,第二行对应
全同粒子体系
全同粒子的全部内禀性质(静质量,电荷,自旋,磁矩,寿命)完全相同,全同粒子不可分辨
全同性假设:全同粒子体系中任意两个全同粒子的交换,都不改变体系的物理状态
任意交换两个全同粒子,体系的波函数或者不变,或者只改变一个符号交换算符 ,本征值为
玻色子和费米子
玻色子:自旋为 的整数倍, 子(S=0),光子(S=1),具有对称波函数
玻色子满足对易规则,体系遵从玻色-爱因斯坦统计
费米子:自旋为 ℏ的半整数倍,电子、质子、中子( ) ,具有反对称波函数
费米子满足反对易规则,体系遵从费米-狄拉克统计
复合粒子
玻色子构成:玻色子
偶数个费米子构成:玻色子
奇数个费米子构成:费米子
全同性假设对哈密顿量的要求
任意交换两个全同粒子,体系的哈密顿量不变。
交换对称和反对称波函数的构成
单粒子:
二粒子体系:
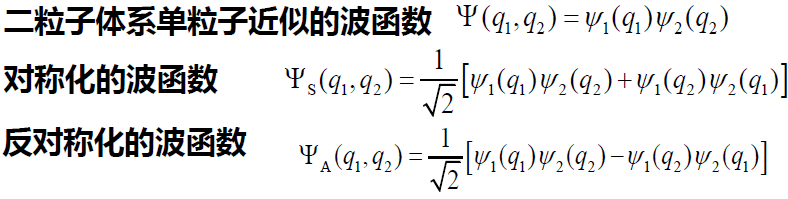
两个独立的玻色子:
两个独立的费米子:
N粒子体系
玻色子:

费米子:
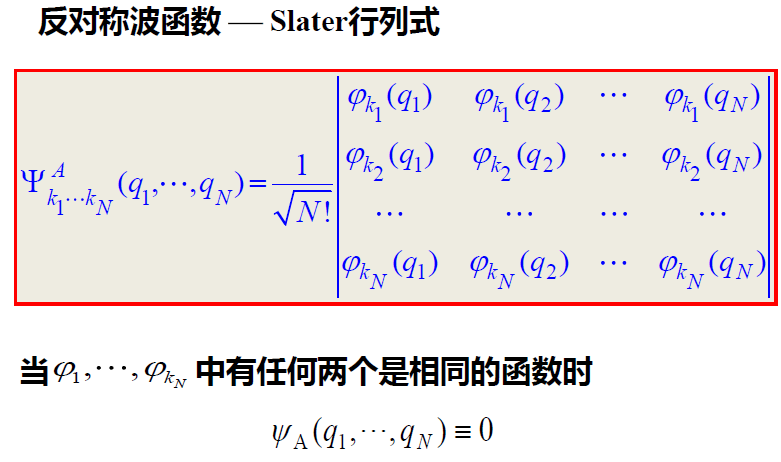
Pauli不相容原理:不可能有两个或更多的费米子处于完全相同的量子状态中。
自旋单态、三重态及纠缠态
单体近似下两电子的自旋函数是每个电子自旋函数的积
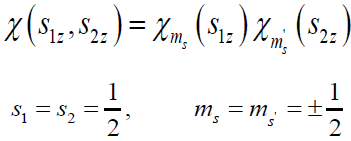
由无耦合表象 的基底可以构成四个具有确定对称性的自旋波函数

纠缠态
可分离态
由两个粒子组成的复合体系的量子态,如果能够表示为每个粒子的 量子态的乘积,则称为可分离态
纠缠态
由两个粒子组成的复合体系的量子态,不能表示为每个粒子的量子态的乘积,则称为纠缠态
角动量合成
两角动量相互独立 ,则它们的分量相互对易,矢量和 也是一个角动量算符,称为总角动量,它满足角动量的一半关系
对易关系:
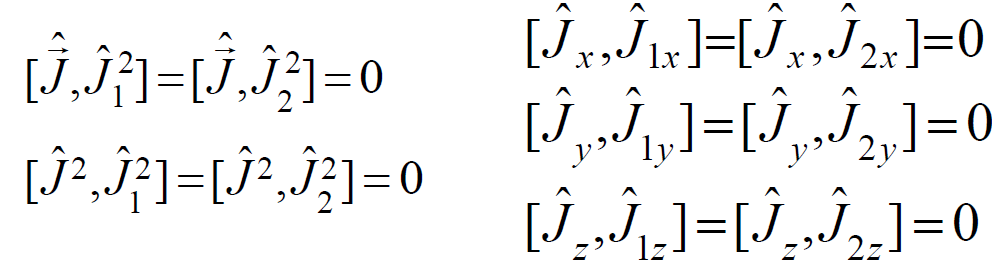
角动量体系的力学量完全集
耦合表象:
基底:
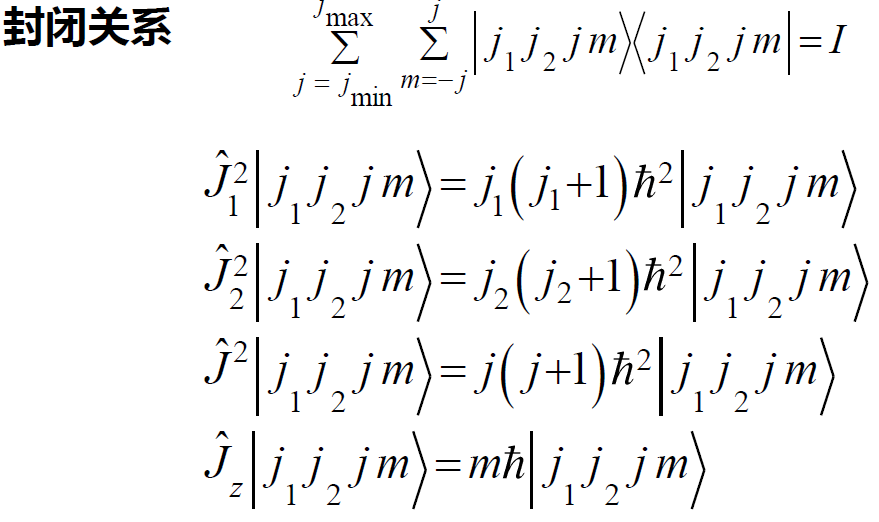
非耦合表象:
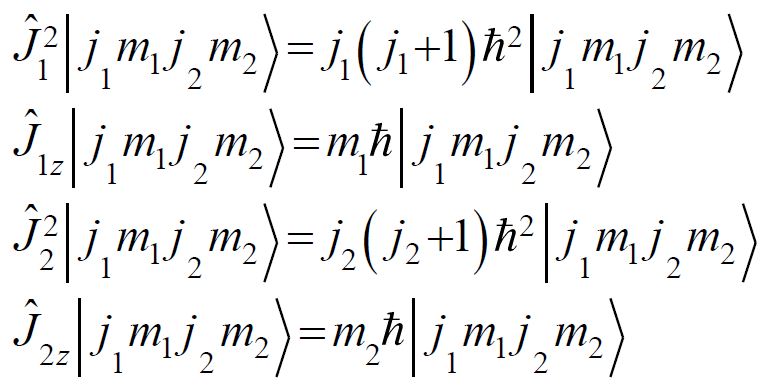
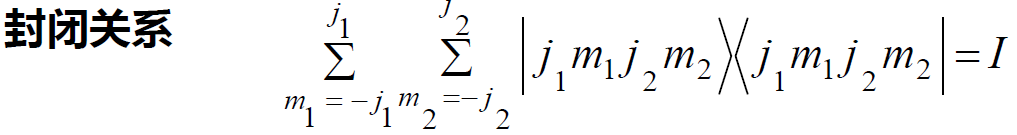
对于总角动量的取值j,如果 ,则