- 注意常将要待求解的量放置到三角形中再求解;
- 注意立体问题平面化的策略;
解三角形
解三角形概念
已知三角形中的一部分边和角,求其余的边和角的过程即为解三角形;
工具:正余弦定理
正弦定理
内容
自然语言
在一个三角形中,各边和它所对角的正弦的比相等;
符号语言
证明
变形[重点]
边的形式
角的形式
比例形式
连比形式
注意比例因子的引入; ,则
求解类型
已知两角及任一边,求其余两边和另一角;
已知两边和其中一边的对角,求另一边的对角,进而求得其余的边和角。
射影定理
与三角形相关的公式【注意】
内角和定理
互余
互补
三角函数关系[和差角公式在三角形中的应用]
互余
互补
余弦定理
内容
自然语言
三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
符号语言
变形
角的形式1
角的形式2
求解类型
已知两边及夹角,求第三边,进而求其余两角。
已知三边,求三个内角。
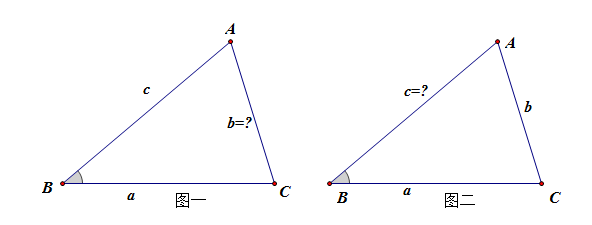
图2的盲点:已知两边及一边的对角,求第三边
学生常用思路:由 ,求得角A,再求角C,再用 求边c
提醒思路:由 ,解关于c的一元二次方程即可
三角形
( 内切圆半径)
关联
普通三角形中
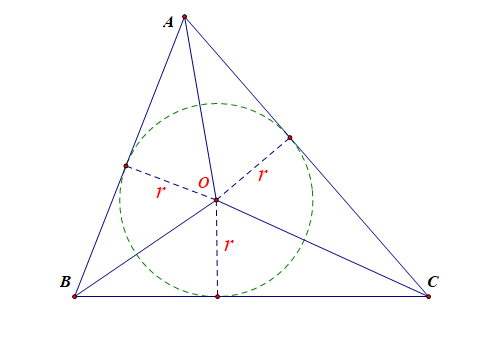
中,
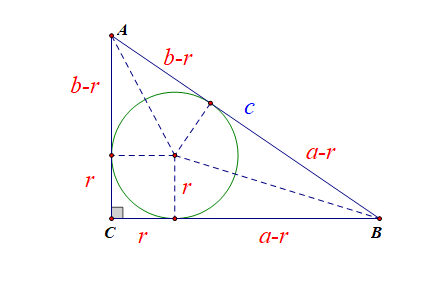
割补法
平面图形割补法
立体图形割补法
题型列举
-
判断三角形的个数
形的角度
数的角度
-
判断三角形形状
是 为锐角三角形的必要不充分条件
是 为钝角三角形的充分不必要条件
是 为直角三角形的充分不必要条件
几个重要结论
-
求三角形的角边
策略:角化边或边化角;
结合正余弦定理
-
求三角形周长类的取值范围
关联到三角函数的图像和性质应用题型了
-
解三角形实际应用
求不可到达的距离
求不可测量的高度
测量角度
引申到求速度,求时间,求方向角等