
使用拉普拉斯算子代表 像素 I(i,j)的信息/平滑程度。L(i,j)的信息等于它的上下左右四个像素之和减去该像素的四倍。
| Note on paper "image inpainting - siggraph 2000" |
Image inpainting
IDEA
main idea
prolong the isophote lines arriving at
while maintaining the angle of "arrival"
prevent prolongation lines from crossing each other
how experts inpaint
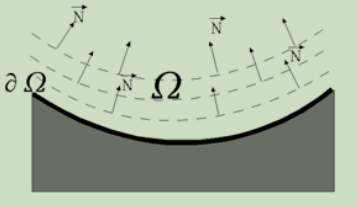
global picture -> how to fill in the gap
structure of is continued into the gap, contour lines
fill with color, matching those of
paint small details(texture)
learn lesson from expert
simultaneously and iteratively perform the steps 2 and 3
METHOD
general form
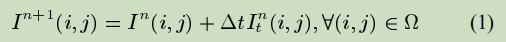
evolution equation runs iteratively inside
is the rate of improvement, is the update
design the update
smoothly propagate information from into
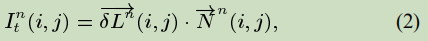
is the propagation information
measures the change of
algorithm converge
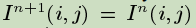
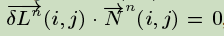 means has been propagated in the direction
means has been propagated in the direction
express the information
since we want the propagation to be smooth, should be an image smoothness estimator
use discrete implementation of the Laplacian as estimator

使用拉普拉斯算子代表 像素 I(i,j)的信息/平滑程度。L(i,j)的信息等于它的上下左右四个像素之和减去该像素的四倍。
express the direction
a bad choice: "shrinked version" of
by the belief that a propagation normal to the boundary would lead to the continuity of the isophotes at the boundary

fail to reconstruct the local image geometry
a suitable choice: the isophotes directions
by the belief that isophotes tend to align with
bootstrapping problem: it's easily recover the gray level image from its isophote direction field
use a time varying estimation of the isophotes direction field
% EXTRACTING ISOPHOTES FROM AN IMAGE
%
% Usage: [ I, theta ] = isophote( L, alpha );
%
% Argument: L - Luminance of the input image [0 255]
% alpha - Threshold of isophotes [0 1]
%
% Returns: I - Magnitude of the isophotes [0 1]
% theta - Angle of the isophotes [-pi/2 +pi/2]
% Vahid. K. Alilou
% Department of Computer Engineering
% The University of Semnan
%
% December 2014
function [ I, theta ] = isophote( L, alpha )
L = double(L)/255; theta=zeros(size(L));
[Lx,Ly] = gradient(L);
I = sqrt(Lx.^2+Ly.^2);
I = I./max(max(I));
T = I>=alpha;
theta(T) = atan(Ly(T)./Lx(T));
I(I<alpha)=0;
end
 gives the smallest spatial change(isophotes direction)
gives the smallest spatial change(isophotes direction)
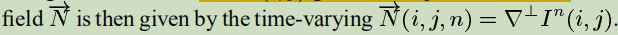
progressively achieves the desired continuity at
use a diffusion process to ensure a correct evolution of the direction field
every few steps, we apply a few iterations of image diffusion
periodical curving of lines to avoid them from crossing each other
use anisotropic diffusion to avoid losing sharpness
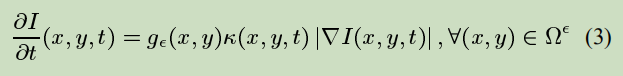
k是等照线的曲率,曲率越大diffusion的系数就越大。g的取值限定了diffusion只在待修复区域进行
compute the change of this value along
Recapping, we estimate a variation of the smoothness, given by a discretization of the 2D Laplacian in our case, and project this variation into the isophotes direction. This projection is used to update the value of the image inside the region to be inpainted.
DETAIL
preprocessing
given a being restored image and its mask
the whole original image undergoes anisotropic diffusion smoothing
to minimize the influence of noise on the estimation of the direction of the isophotes arriving at
inpainting loop
only the values inside are modified
discrete implementation
first compute the 2D smoothness estimation L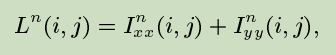
then compute , the projection of onto the direction
Every few iterations, a step of anisotropic diffusion is applied
repeated until a steady state is achieved
color image
Color images are considered as a set of three images, and the
above described technique is applied independently to each one
use a color model to avoid the appearance of spurious color