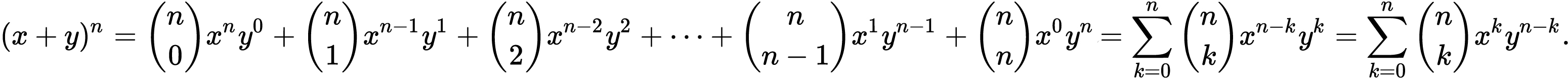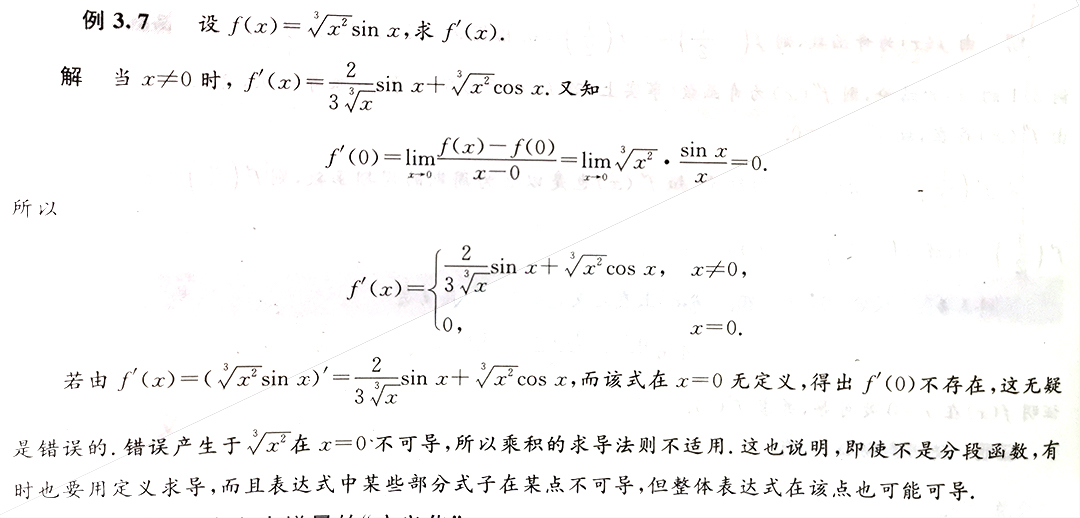我的数学
向量
平面向量
a,b同向
a,b反向
减法
共起点
尾尾相接
指向被减
数量积
几何意义:
结果是个数量,不是向量
坐标运算
三角形内
中线
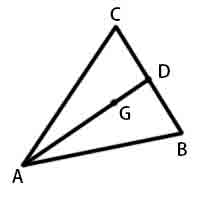
重心:
角分线
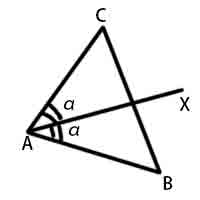
集合
三个特点:确定性,互异性,无序性
常用集合
非负整数集合N {0,1,2,3,4...}
正整数集合 或 {1,2,3,4...}
整数集合Z {0,1,-1,2,-2...}
有理数集合Q
实数集合R {x|数轴上点的坐标}
全集U
子集
若 且 则A=B
若 且 ,则A真包含于B,
有n个元素的合集 ,子集的个数为 个,真子集的个数为 个,非空真子集的个数为 个
补集
若A=B,则 ,反之也成立
Card(S):S的元素个数
排列组合
排列
组合
函数
有界性
单调性
函数f(x)与f(x)+c(c为常数)具有相同的单调性
k>0时,函数f(x)与kf(x)单调性相同
k<0时,函数f(x)与kf(x)单调性相反
若f(x)恒为正值或恒为负值,则f(x)与 具有相反的单调性
若f(x),g(x)都是增函数(减),则f(x)+g(x)是增函数(减)
若f(x),g(x)都是增函数(减),则 当两者都恒大于零时,是增函数(减);当两者都恒小于零时,是减函数(增)
复合函数y=f(g(x)):同增异减
奇偶性
奇函数f(-x)=-f(x) 偶函数f(-x)=f(x)
奇函数f(x)如果在原点有定义,则f(0)=0;
若一个函数既是奇函数又是偶函数,则f(x)=0
四则运算
奇 奇=奇,偶 偶=偶
奇x/奇=偶,偶x/偶=偶
奇x/偶=奇
复合
奇【偶】=偶,偶【奇】=偶,偶【偶】=偶,非【偶】=偶
奇【奇】=奇
若f(x)为偶函数,则
多项式 的奇偶性:
只有奇次幂,f(x)为奇函数
只有偶次幂,f(x)为偶函数
有奇有偶次幂,f(x)非奇非偶
二次函数 若为偶函数 b=0
的一般方法:
※
对称性(自变量的和为常数)
对称轴为
对称中心为
周期性(自变量的差为常数)
函数周期性、奇偶性、对称轴的关系
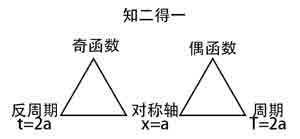
凹凸性(分大下凸)
部分初等函数
指数函数
基本性质
对数函数
基本性质
换底公式:
some special
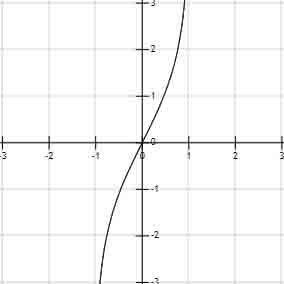
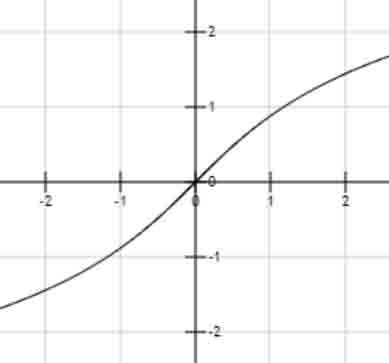
奇函数!!!
绝对值
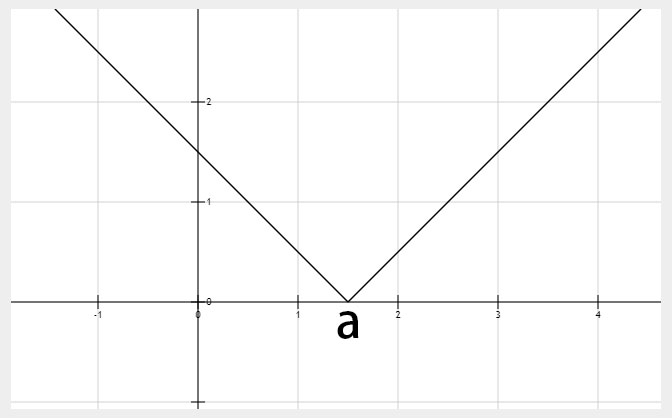

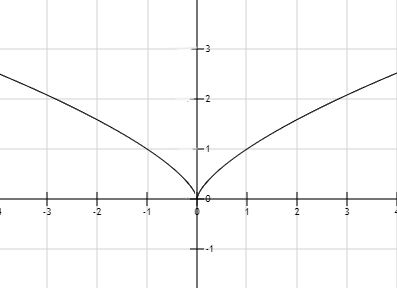
幂函数
形如 的图像,第一象限均类似,根据奇偶性判断二三象限的图像
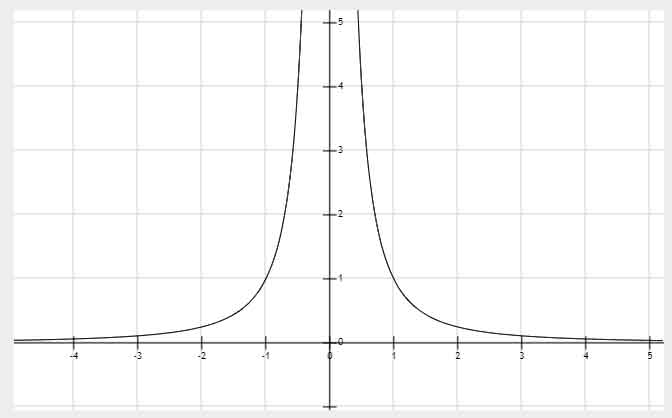


一元二次方程
:正有两个解,负无实数解,=0有一个解
韦达定理
二次函数
对称轴:
最值:
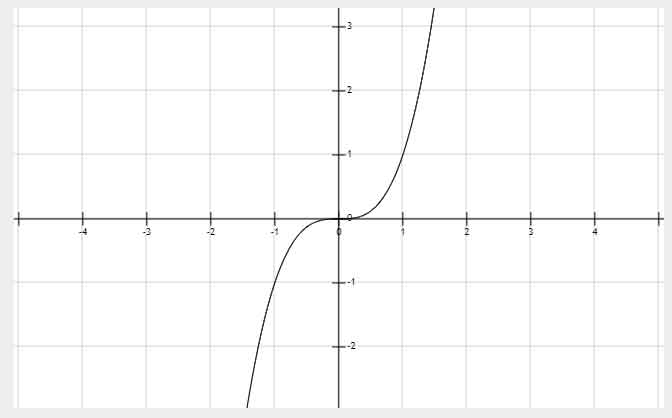
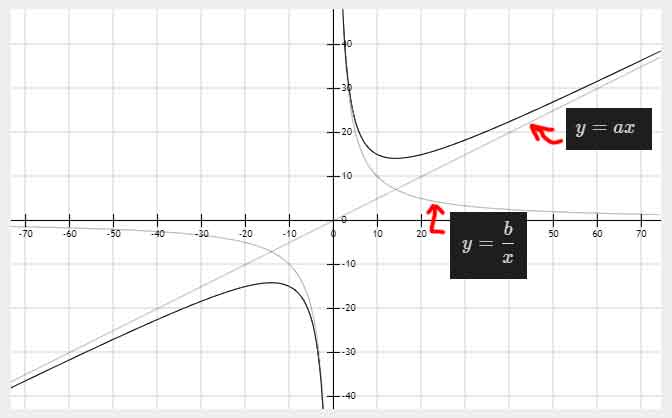
a,b同号,双钩
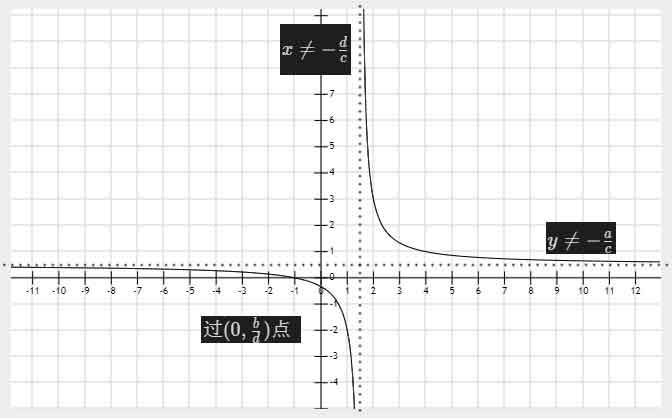
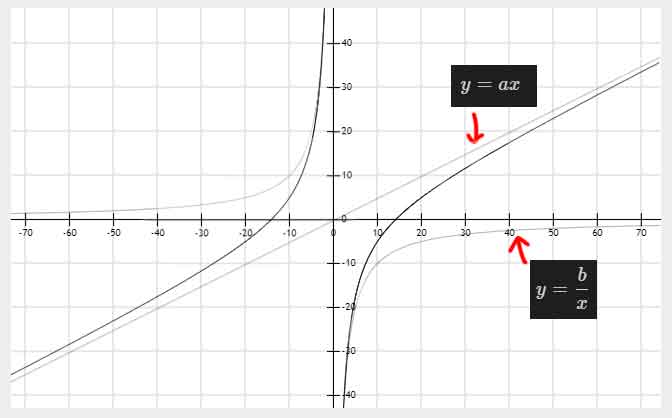
a,b异号,双撇
三角函数
性质
同角三角函数
三角函数六边形

诱导公式(任意角 锐角,奇变偶不变、符号看原来这个函数的象限)
函数名不变,符号看象限
函数名改变,符号看象限
函数 的特征
两角和差的正弦、余弦、正切公式
倍角公式
升降幂公式
半角公式
万能公式
和差化积
积化和差
辅助角公式
,其中 满足
tan ϕ = b a \tan\phi=\frac{b}{a} 。注意:若将a框定在>0,则可将 框定在 内便于计算
特殊锐角三角函数
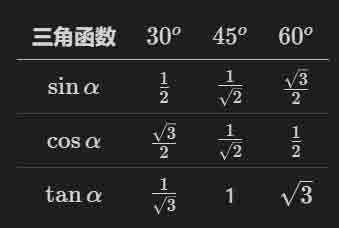
分角的一个办法

部分图像
cot(x)
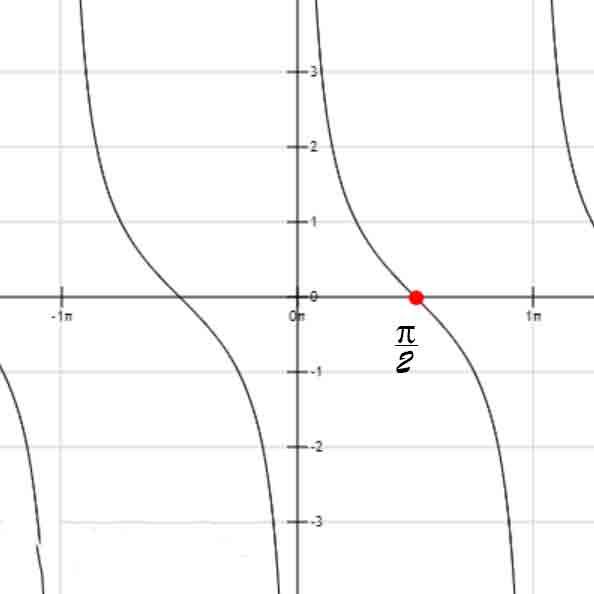
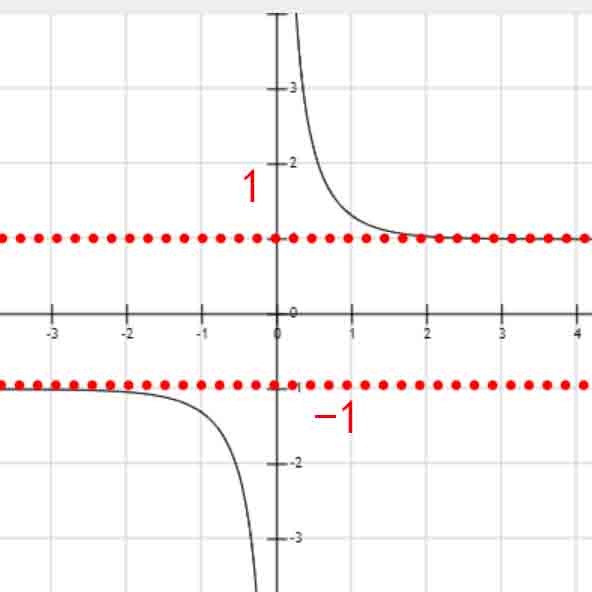
sec(x)
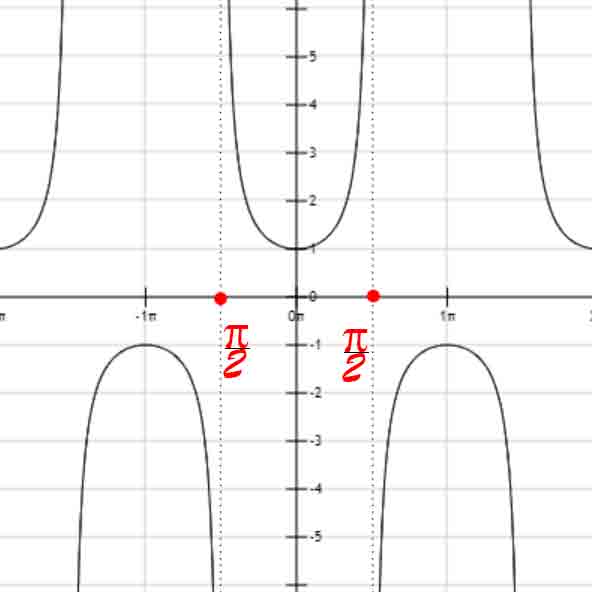
csc(x)
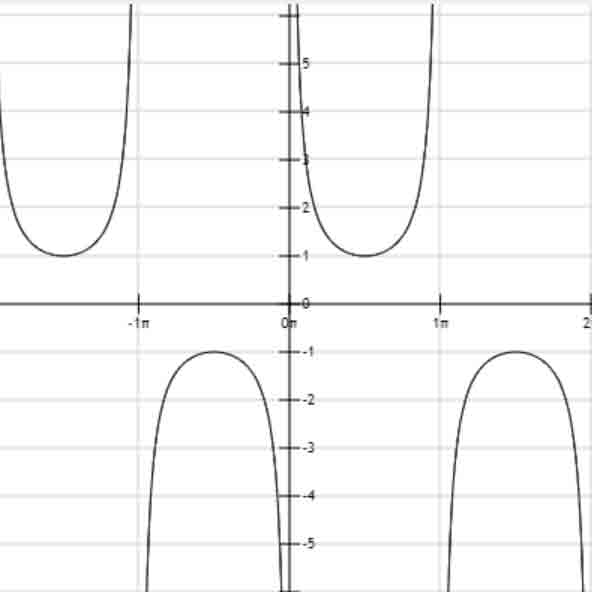
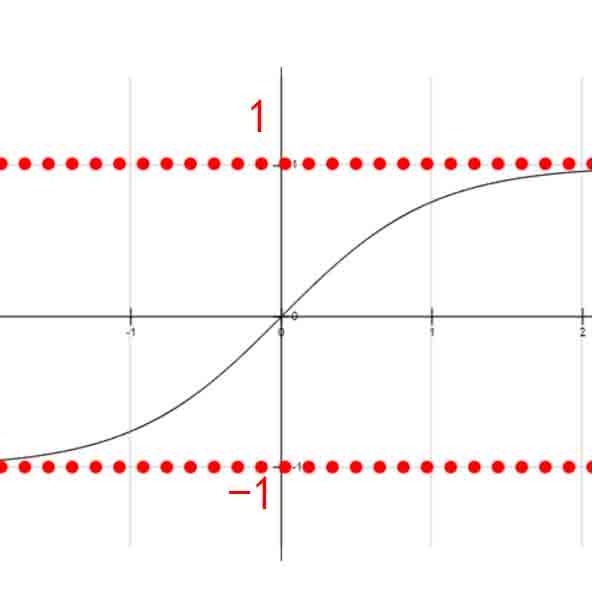
arcsin(x)
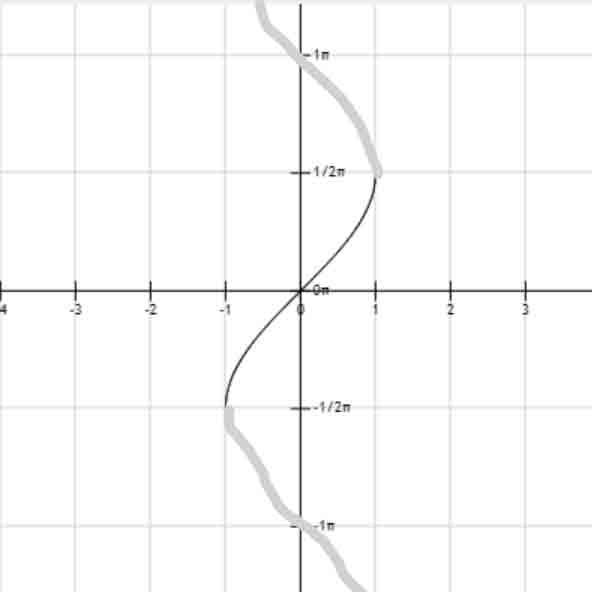
arccos(x)
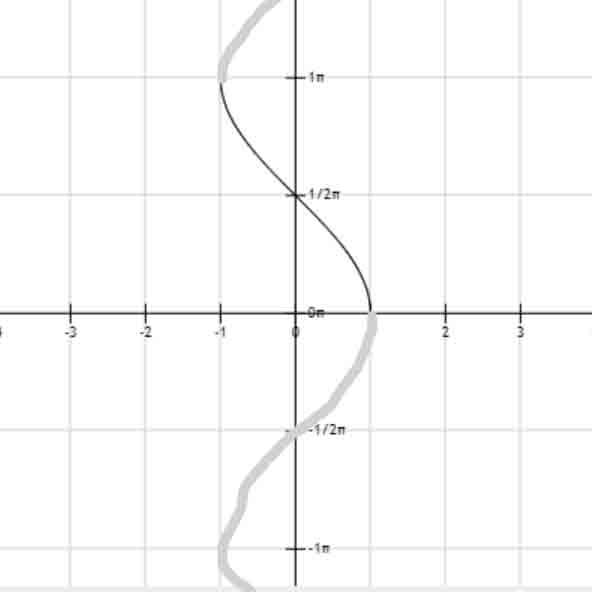
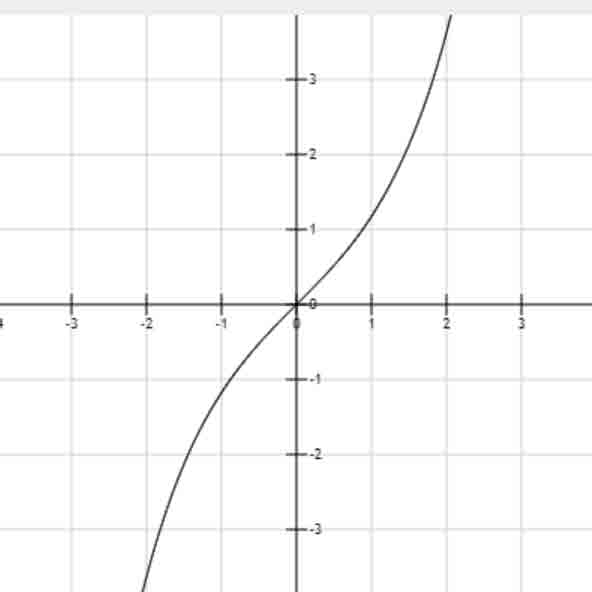
arctan(x)
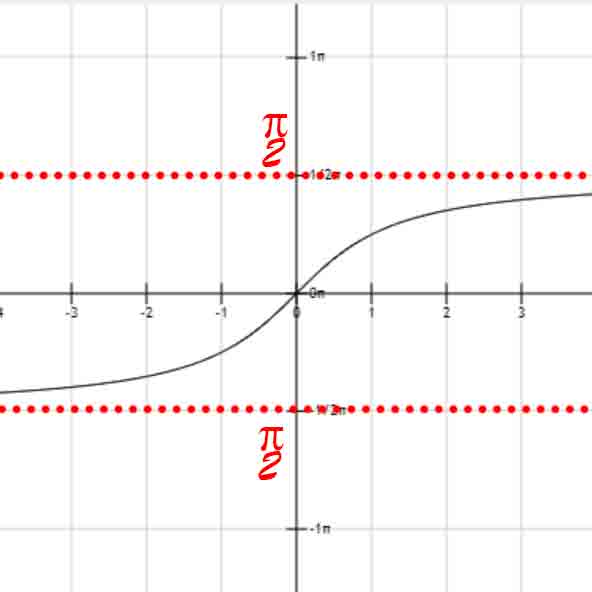
arccot(x)
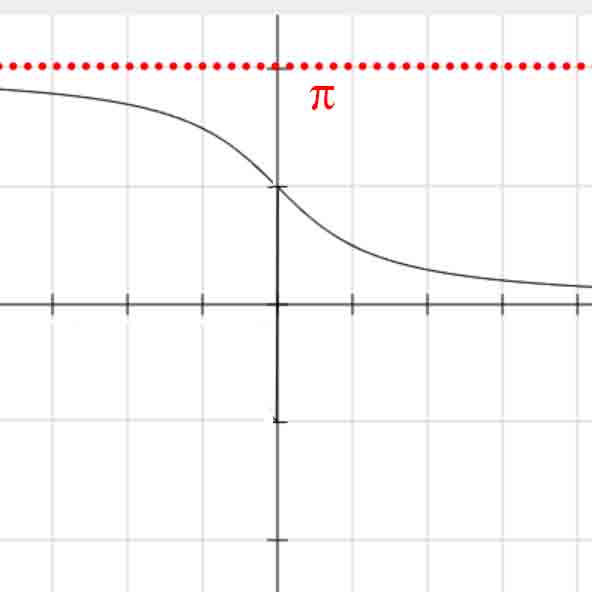

符号函数
取整函数—向左取整
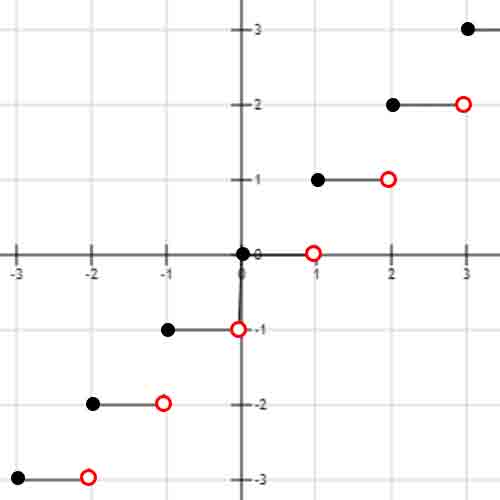
n为正整数
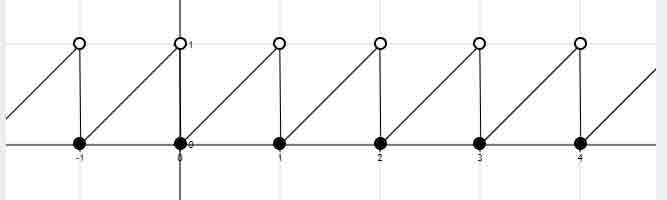
T=1
阶乘
双阶乘
几何
直线
直线点斜式
三角形
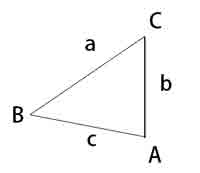
大边对大角,小边对小角
构成条件
可构成三角形:
直角:
锐角:
钝角:
正余弦定理
正弦定理
(外接圆半径)
余弦定理
面积S
六心
内心
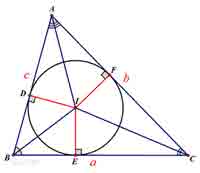
内切圆圆心
角分线交点
到三边等距
外心
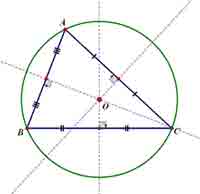
外接圆圆心
中垂线交点
到三顶点等距
重心
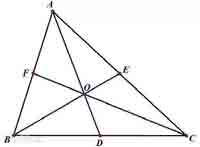
中线交点
分中线2:1(重心到顶点的距离与重心到对边中点的距离之比为2:1)
(在平面直角坐标系中,重心的坐标是顶点坐标的算术平均)
到三个顶点距离平方和最小
重心和三角形3个顶点组成的3个三角形面积相等
垂心
三条垂线交点
中心
正三角形四心重合
旁心
角分线,外角分线的交点
到三边等距
多边形
一个n边形从一个顶点出发有(n-3)条对角线,所有对角线的数量是
n边形内角和等于
多边形的外角和恒等于 ,与边数n无关
正n边形的每个内角等于 ,每个外角等于
梯形面积:(上底+下底)X高/2
圆
扇形
圆心角
扇形弧长公式:
圆锥
体积=同底等高圆柱的
极限
数列极限
定义——

数列 ,子列
子列极限相同:
判断发散的方法
发散子列
两个子列极限不同
注意这里是任意子列收敛于相同的极限才可以反推回去
极限的存在,不考虑前有限项极限的情况,着重考虑极限时情况是怎么样的
构造
放缩法

寻找一个已知的极限形式
阿格朗日法
中值定理
收敛数列性质
唯一性
存在,则a唯一
有界性
存在 有界
表述方法:
找界:找常数的界,不能带n,数列的首项也可以
保号性
保号性:
(w是个数字)
运算法则
公比小于1的等比数列前n项和的极限,
极限存在准则
注意:
推论:
考法
无穷项相加
∑ i = 1 n u i = u 1 + u 2 + . . . + u n , n 为 ∞ {\displaystyle \sum_{i=1}^{n}{u_i} }=u_1+u_2+...+u_n,n为\infty

注意是i,不是n
老大老小合力才行
有限项相加
∑ i = 1 n u i = u 1 + u 2 + . . . + u n , n 为 ∞ {\displaystyle \sum_{i=1}^{n}{u_i} }=u_1+u_2+...+u_n,n为\infty
老大说了算
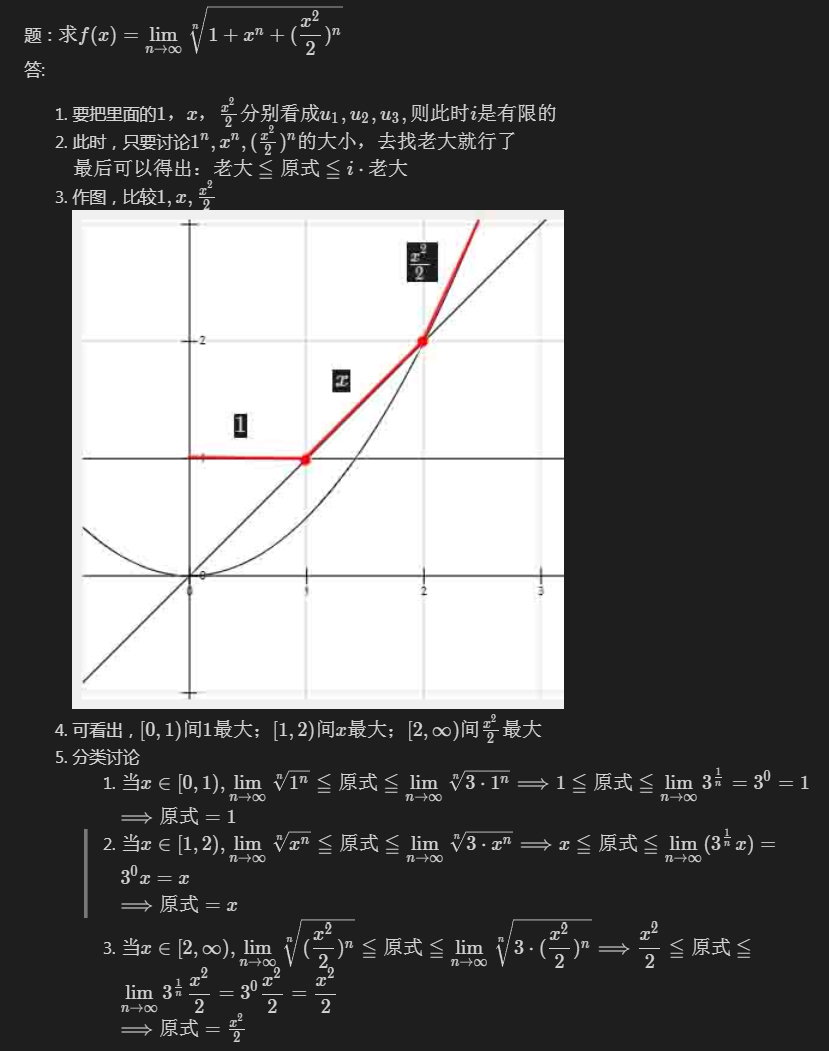
有提示

题目中第一问给出提示 ,第二问求极限
不验等号
※单调有界数列必有极限
①

数学归纳法

①代入n=1时证明成立
②设
③证明
④则当n为全体自然数时,结论成立
※不等式

或许有提示
②上下界
考点
①恒等变形求极限
变换后累加累乘用等比数列的公式再求极限
递归

②单调有界准则
先证单调,再找界
题目中有字眼:证明极限存在并求之,呵呵
③定义法
一般目标明确才用,a已知或者很明显
这个题中,能猜出极限pi,但是如何去构造pi,tan x =0

①放缩
注意:题目中定义域a<n<b,也是放缩!!!
②拉格朗日中值定理
④夹逼准则
求xxx,很直接
放缩型①:动分子不行动分母

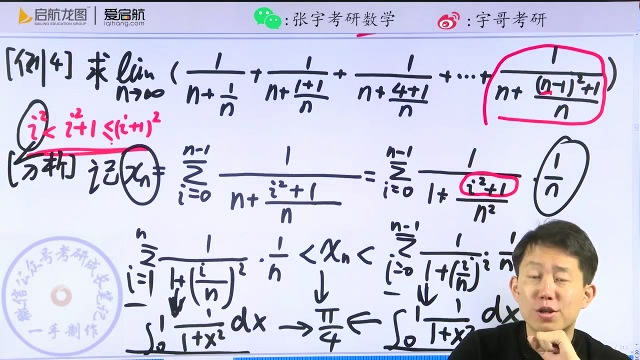
⑤定积分定义
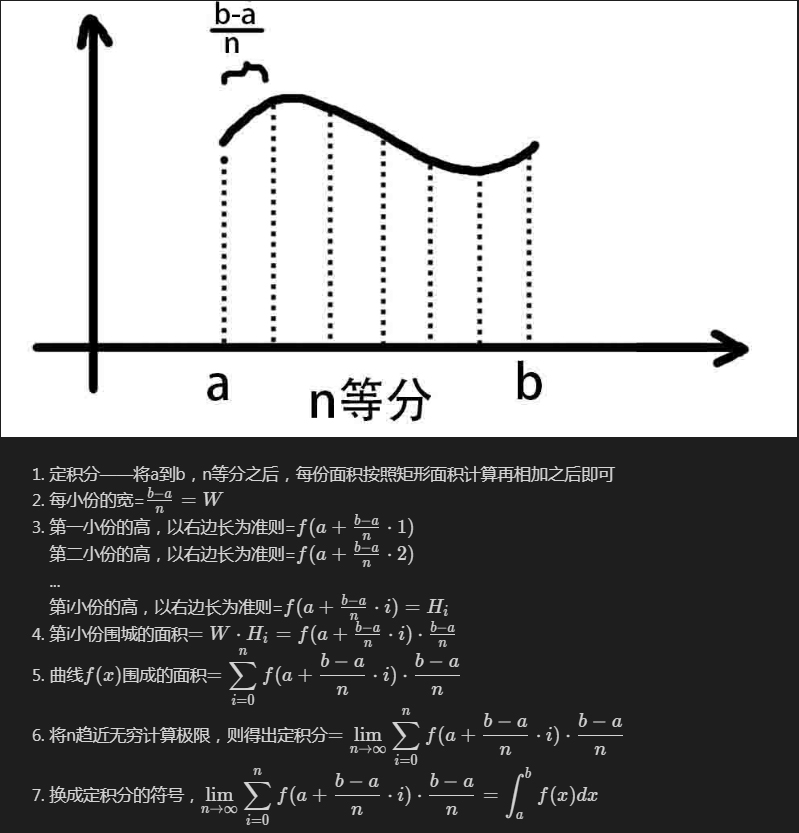



变量型:

放缩型②:放缩后再凑
函数极限
领域定义
开区间
一维:
二维:
函数极限定义
性质
唯一性
注意:

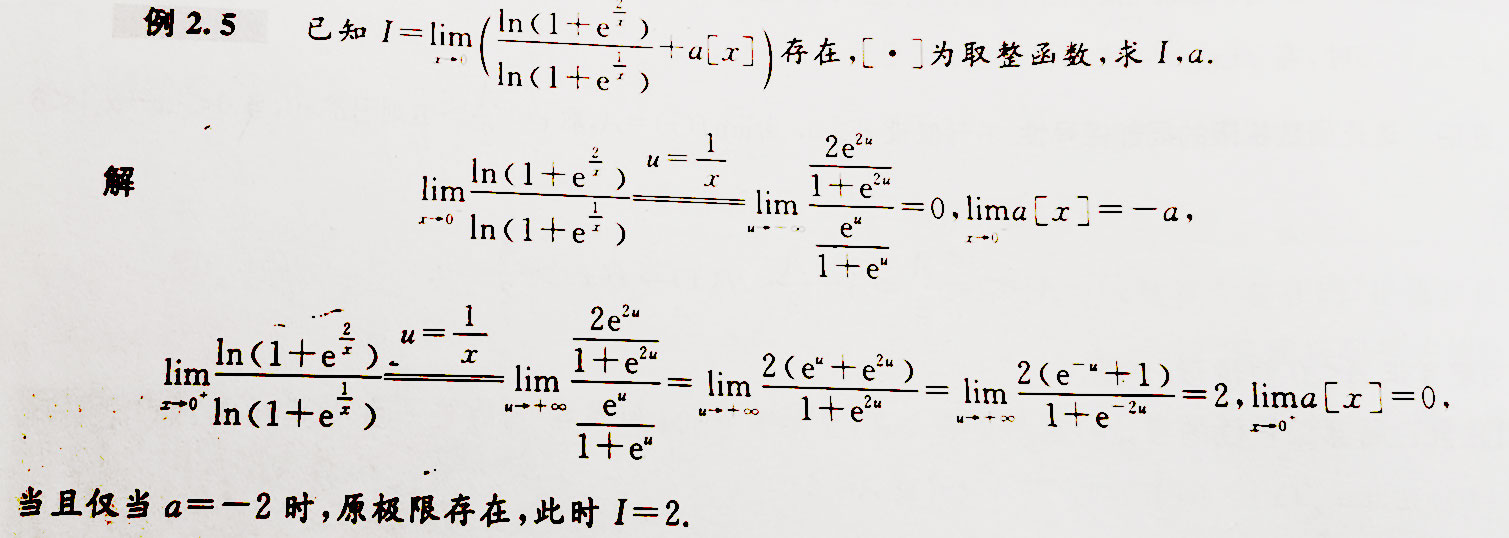
局部有界性(仅是充分条件,非必要条件)
有界函数与有界函数的和、差、积也有界

局部保号性
无穷大、小
小
大
关系
,反之亦然
无穷小比阶

高阶
等价
常用等价无穷小
导数:
导数:
导数:
导数:
导数:
并不是任意两个无穷小都可以比阶
,

无穷小运算规则
m,n正整数有限个无穷小的和是无穷小
有限个无穷小的乘积是无穷小
有界函数与无穷小的乘积是无穷小
加减法——低阶吸收高阶
乘法——阶数累加
非零常数不影响
存在的充要条件
左右极限存在且相等
脱帽法

运算规则
前提是各自都存在!!!

存在准则——夹逼准则
放缩
注意:题目中给的定义域,a<x<b也是放缩!!!
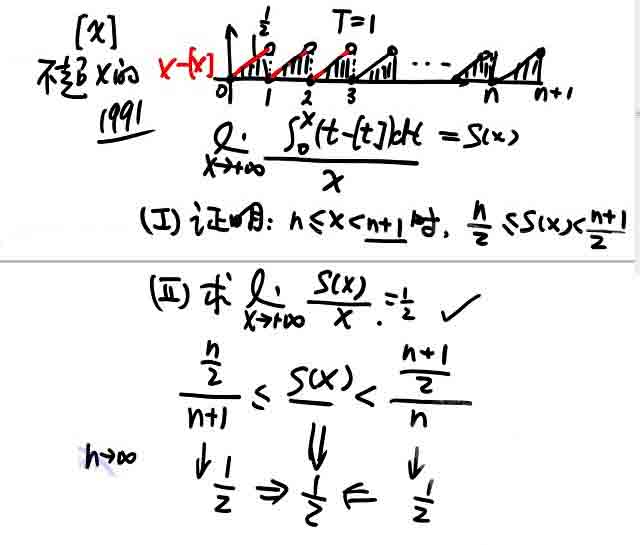
的计算——洛必达法则

不是 不能用
也不一定存在
此时洛必达失效,但是不能证明原式极限不存在右存在,左存在
左存在,右不一定一直洛

函数极限与数列极限——海涅定理
 存在的充要条件是:取
存在的充要条件是:取 定义域内的任意数列{
定义域内的任意数列{ },
}, ,且
,且 不等于
不等于 ,有
,有
x数列化后,f(x)与f(xn)极限相同
数列
some lim
※泰勒展开式
任何可导
主部——第一项
展开原则
展开到几阶? 型
上下同阶
A-B型
幂次最低
将A,B分别展开至系数 不相等的x的最低次幂为止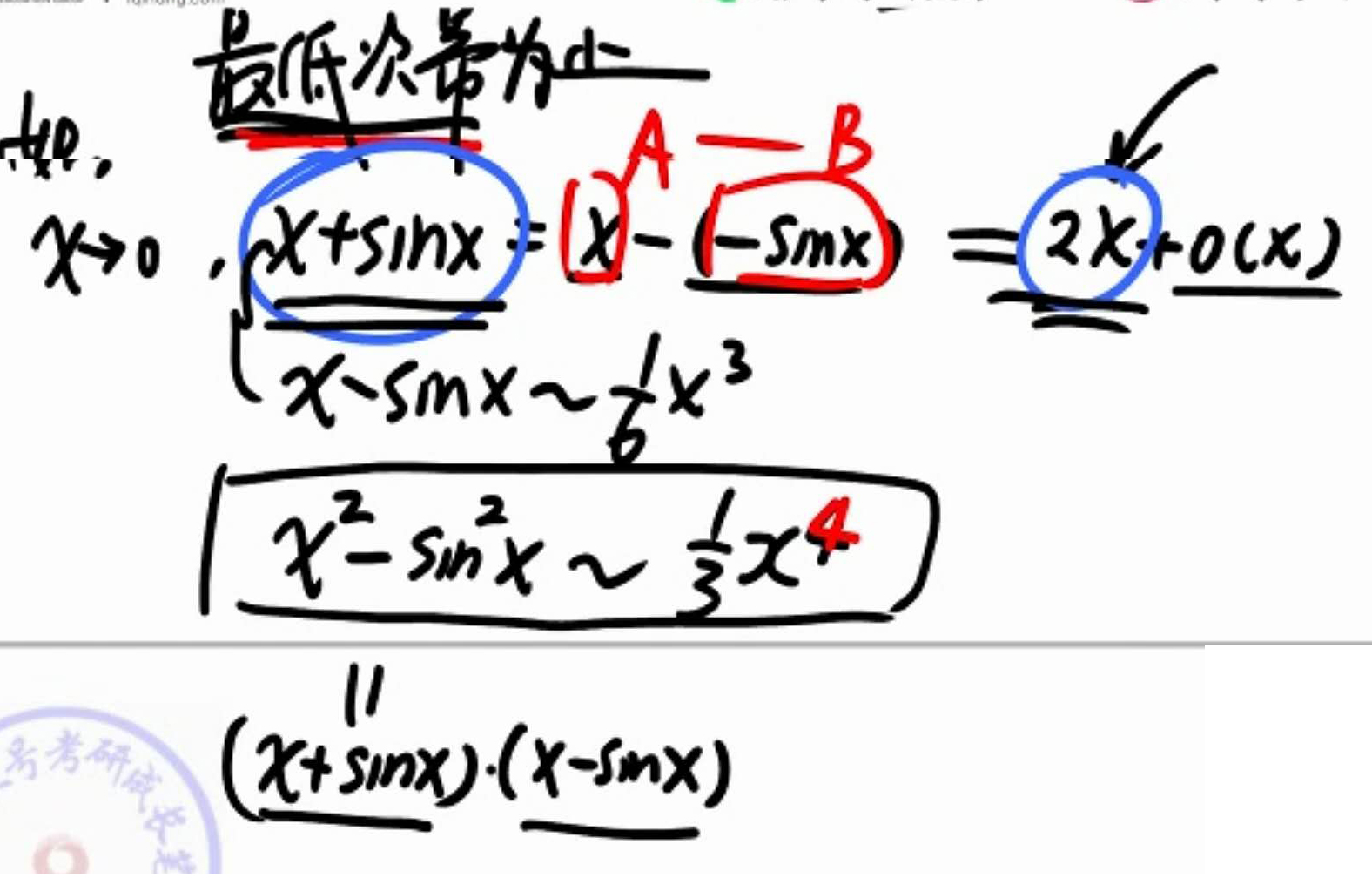
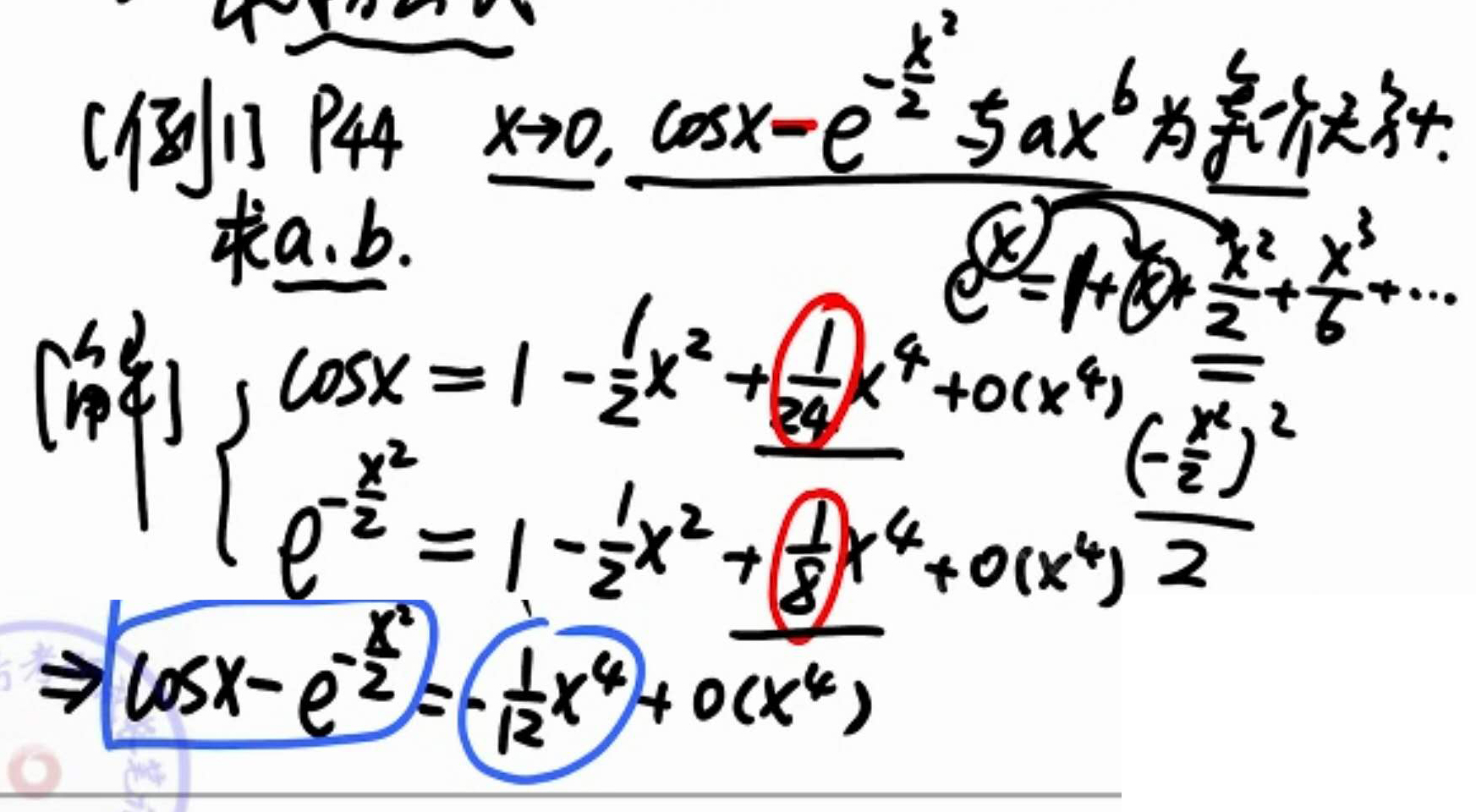
考点
求极限
七种未定型
设置分母的原则,简单因式才下放:
复杂: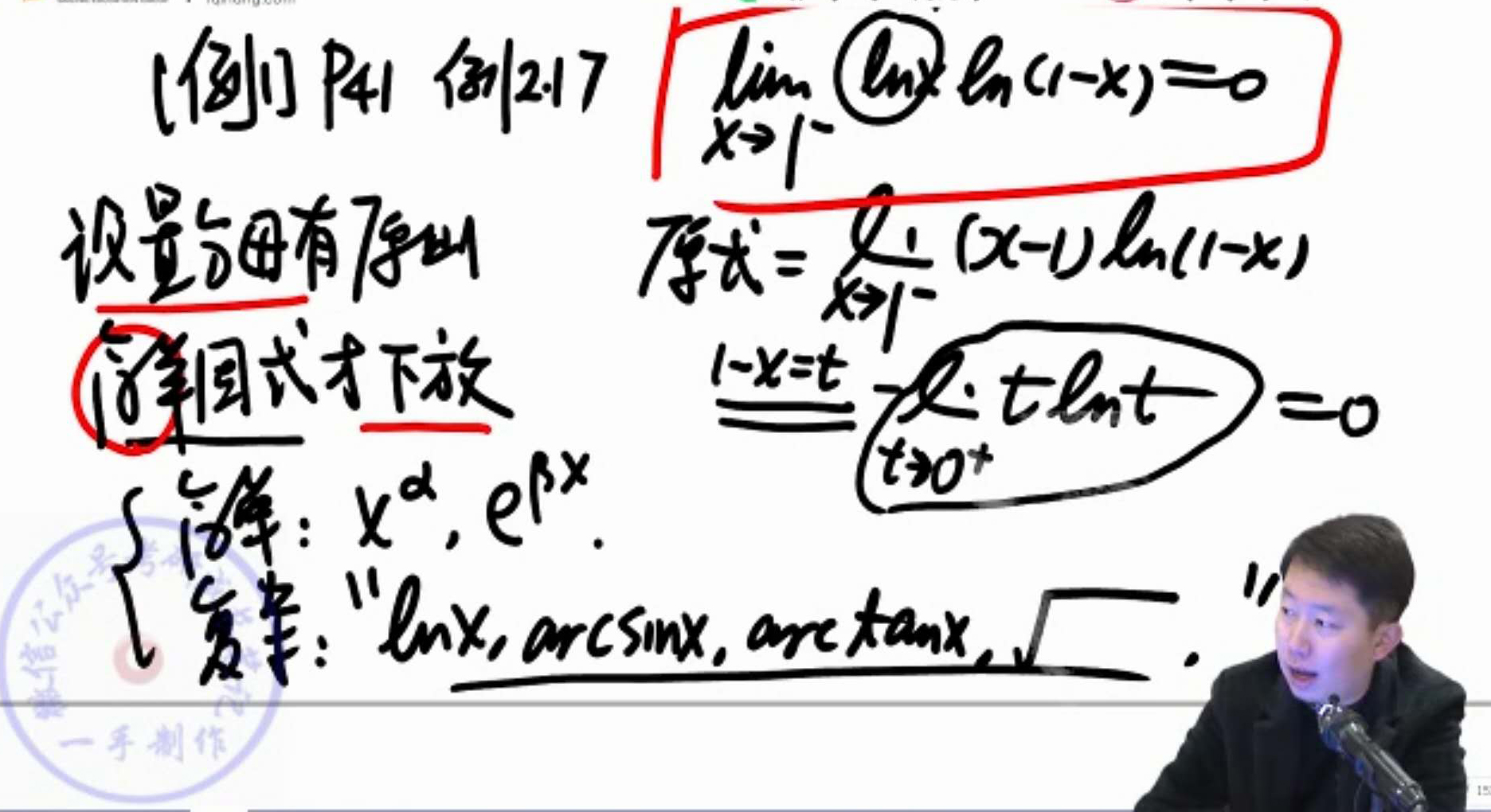
幂指

题型
1.比阶题
2.反问题,反求参数
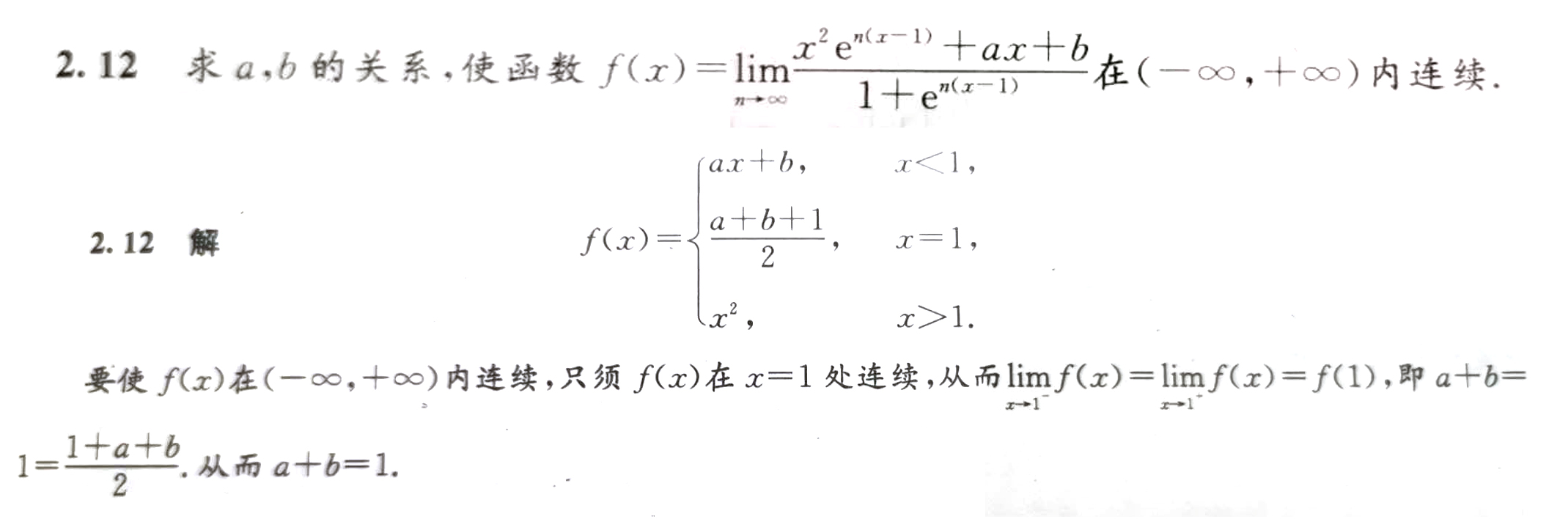
3.已知某一极限,求另一极限
直接把f(x)求出来

寻找两个极限之间的关系

形式
——差函数
——导函数
——积分
洛必达

方法
恒等变形—化简
++--**//
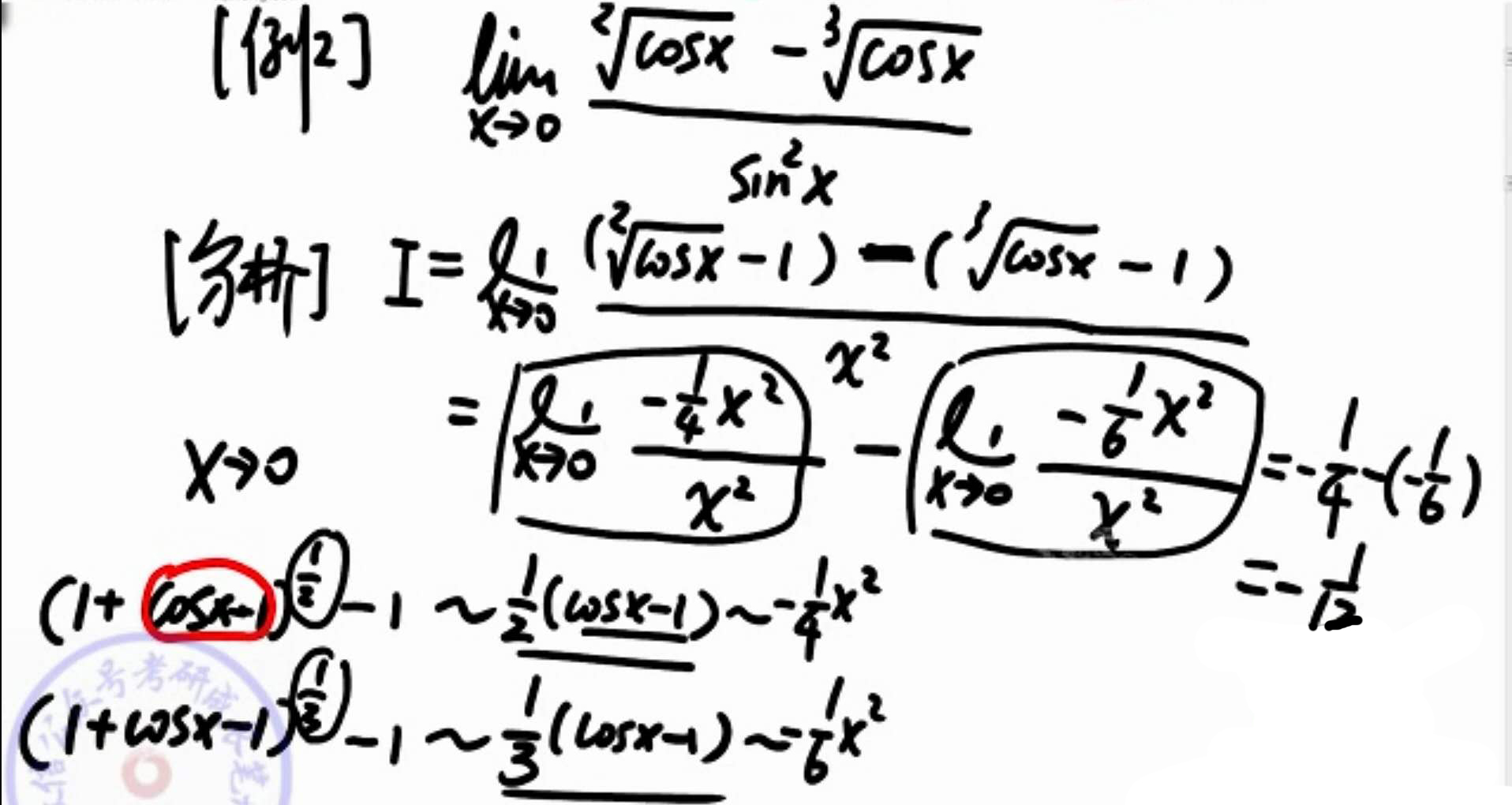
上下同除x

n=1+1+1+...+1(n个)
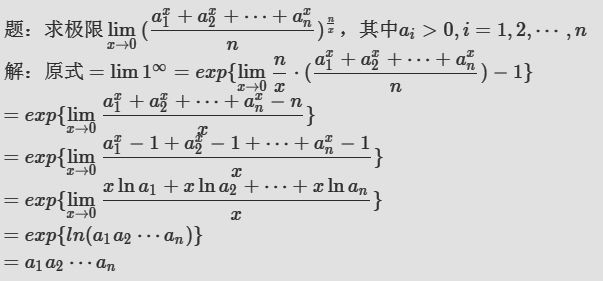
换元

公式

裂项向消


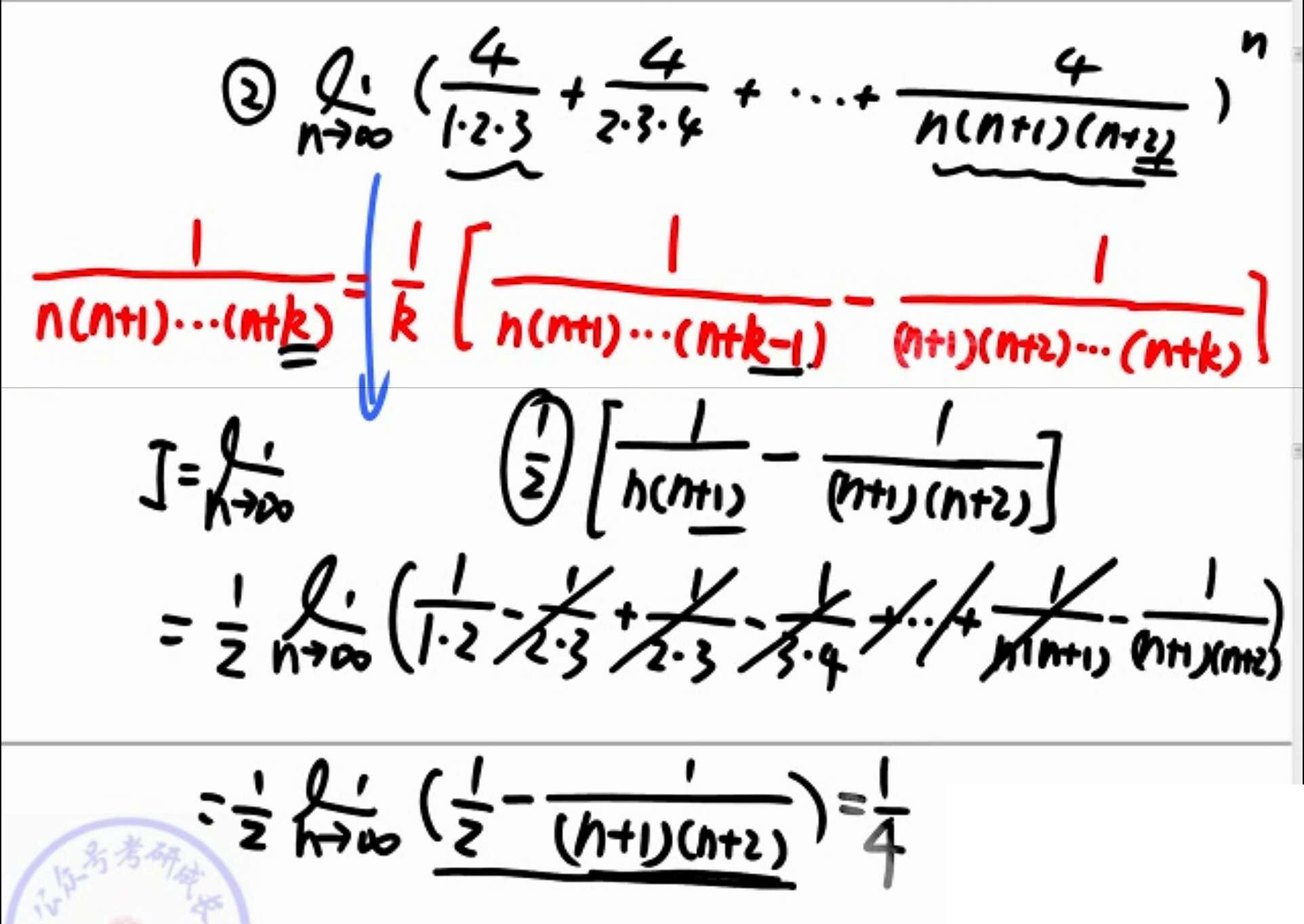
对幂的处理
ln
除一下,统一到一个带幂函数
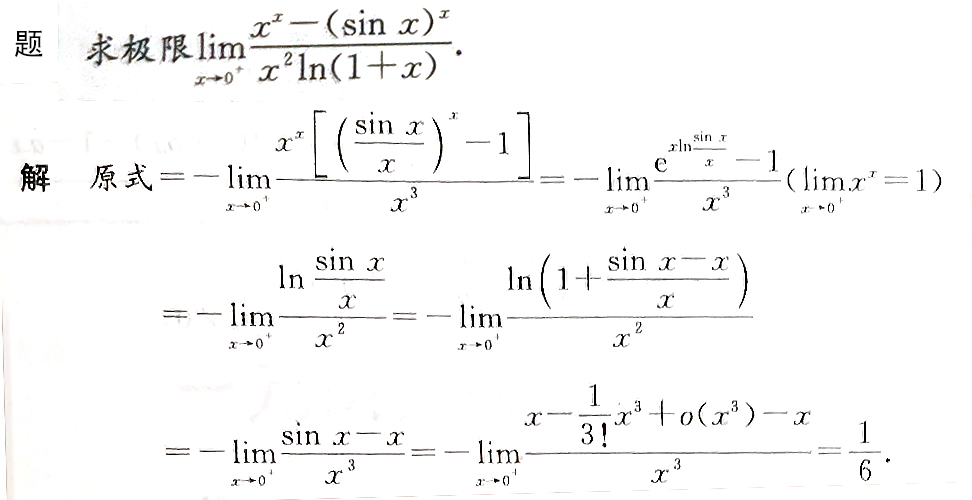
a^n-b^n因式分解
等价无穷小替换(主部)
洛必达

泰勒公式

夹逼准则
当常规的洛必达、泰勒等不行的时候

单调有界准则
综合
不等式
性质
线性规划
直线
>0 右侧
<0 左侧
圆,圆心(a,b)
过(x,y)和(a,b)直线的斜率
一些常用
均值不等式
调和平均数
几何平均数
算术平均数
平方平均数
变形
条件:一正 二定 三相等
①a,b两数都是正数
②ab乘积必须是定值,不能有变量ab
③两数能相等a=b
积定和最小,和定积最大
两正数,和一定,越接近,积越大
两正数,积一定,越接近,和越小
绝对值不等式
连续
定义——极限与值相等
表达方法1:
表达方法2:
※
间断点
第一类
可去
跳跃
第二类
无穷
振荡
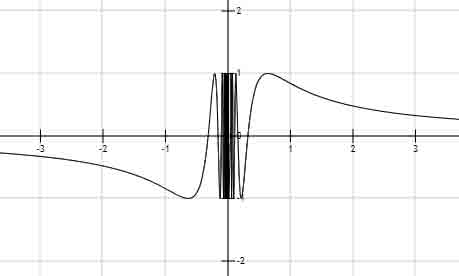
例如 在0处振荡
数列
求 通项
已知递推项

①化简(因式分解)
若 为 a n + 1 = 1 2 a n + 19 的 形 式 若为a_{n+1}=\frac{1}{2}a_n+19的形式
解C
②直接展开
③同形异角(辅助数列)
④转化为同形异角
⑤找规律
求首项( )
求递推
解递推
等差数列
通项公式:
距离首末两项等距的两项和相等,
连续等长片段和仍是等差:
??公差
对称设项方法
n为奇数
设成:a-d,a,a+d
n为偶数
设成:a-2d,a-d,a+d,a+2d
证明方法
公差d常数
通项公式
等差中项:
前n项和:
前n项和
前n个奇数的和是
按项数分类情况
项数为偶2n
项数为奇2n-1
等比数列
通项公式:
,否则不成立
距离首末两项等距的两项积相等,
连续相邻k项
和:等比公比
积:等比公比
对称设项方法
如果为奇数个项数,则可以设
但是如果是四个,不要设 ,因为此时公比 恒正,漏解
证明方法
公比q常数
前n项和:
按项数分类情况
项数为偶2n
项数为奇2n+1
差比互换
中项
若m+n=i+j
错位相减-差比数列
裂项相消
一些数列
平方、立方数列
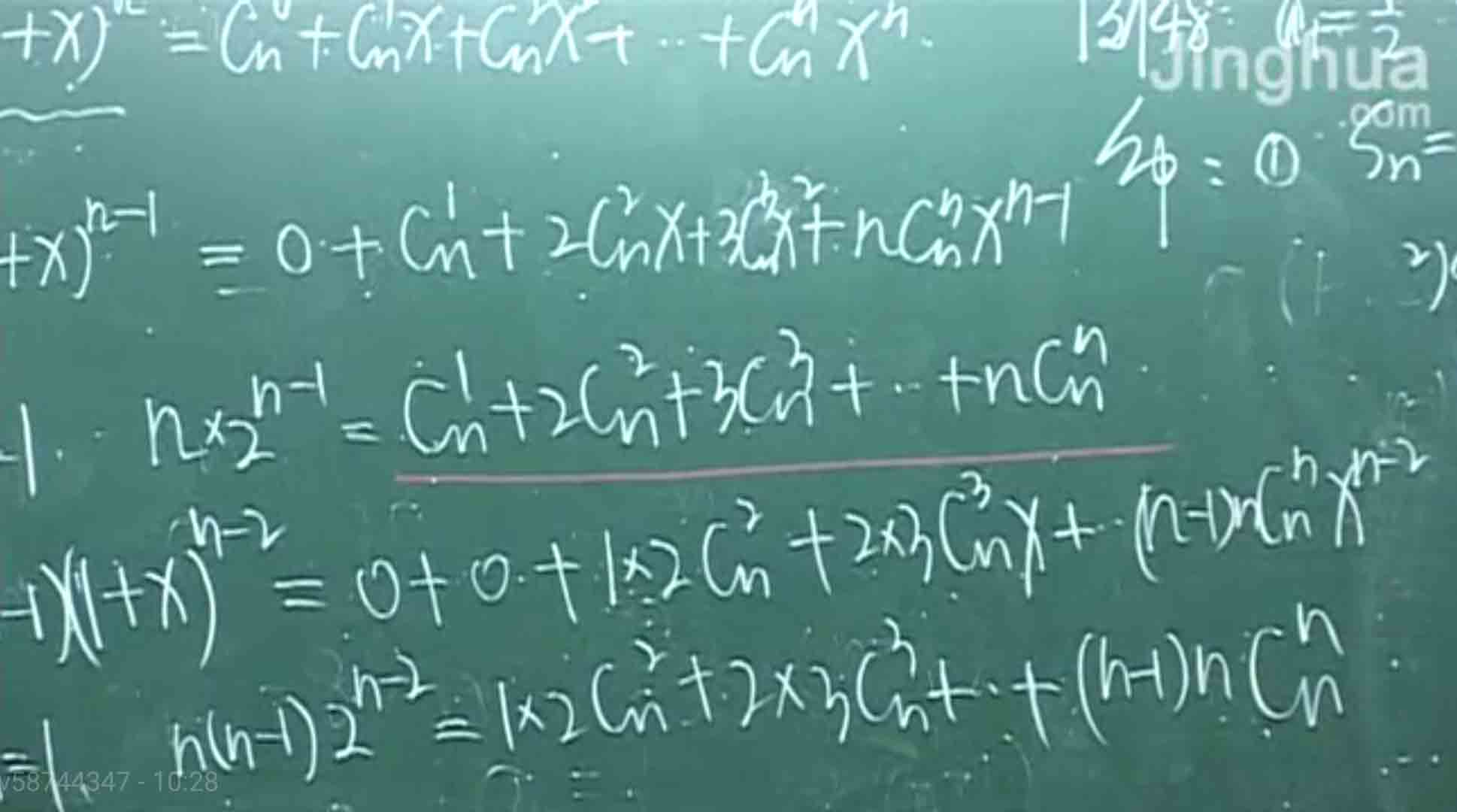
微积分
牛顿莱布尼茨公式:
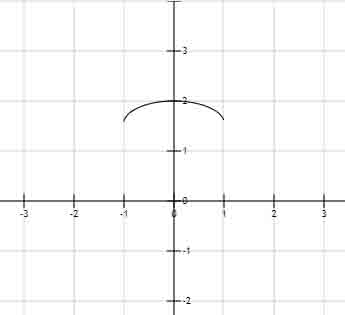
sinx一个拱的面积是2
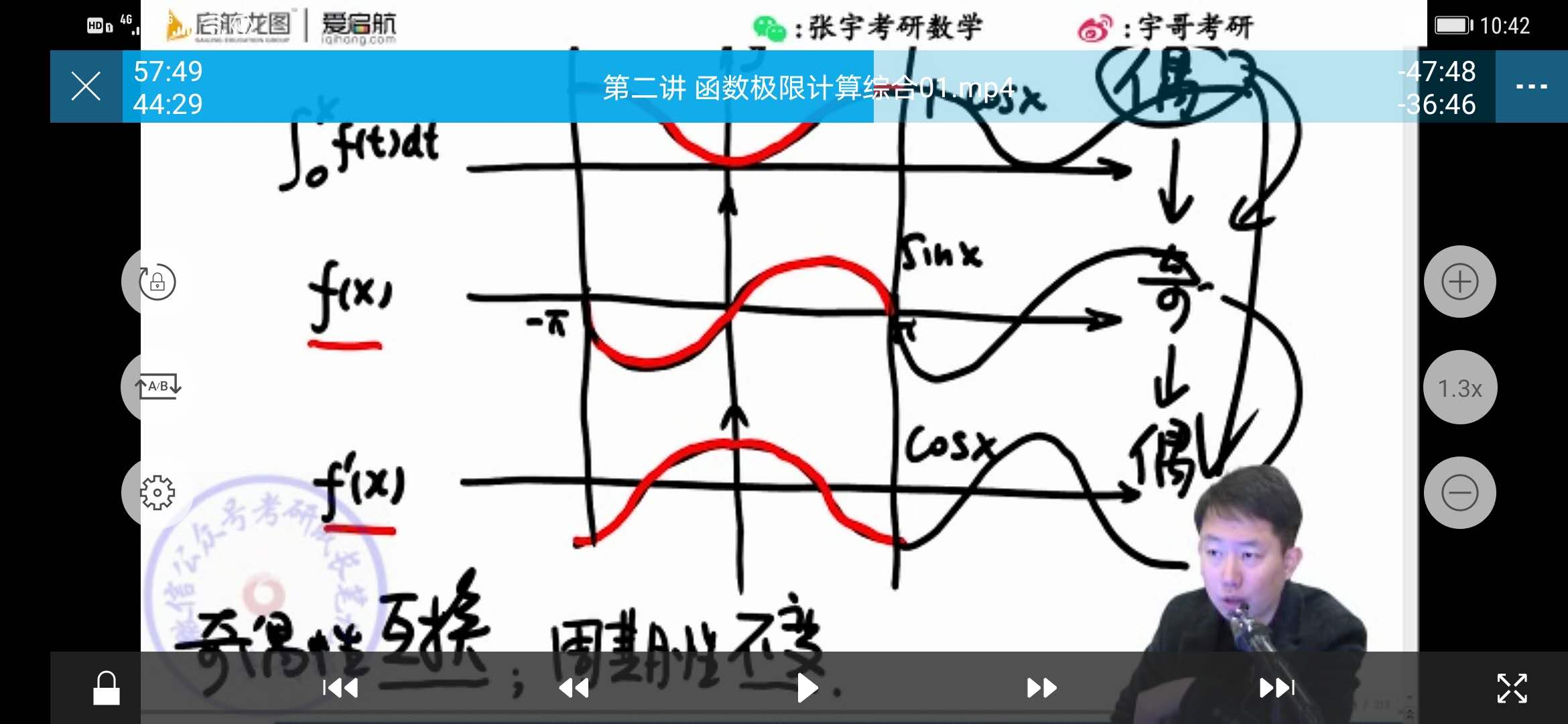
f(x)微分和积分奇偶性互换,微积分后周期性不变
注意积分是0下限的
some tips
二元一次方程组 解的情况
当 时,方程组有唯一一组解
当 时,方程组有无数组解
当 时,方程组无解
比例的性质
基本性质:如果 ,那么ad=bc
合比性质:如果 ,那么
等比性质:若 ,则
因式分解
杨辉三角
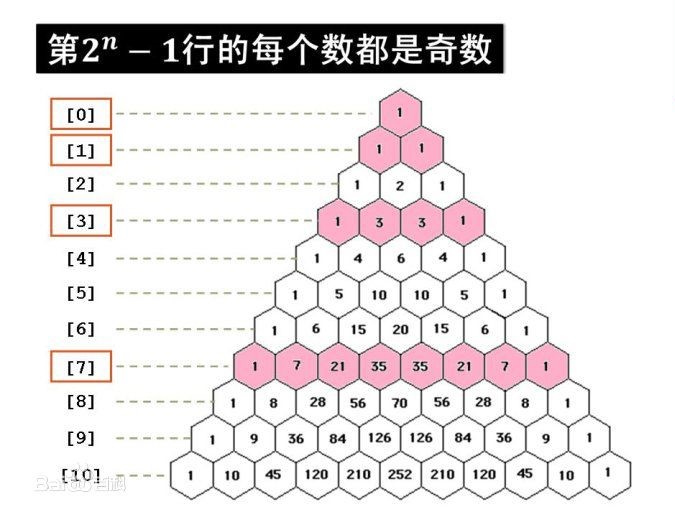
立方和差公式
二项式定理
一元函数微分学
导数定义: 存在 可导
——(瞬时)变化率拉格朗日
莱布尼兹
①换元
广义化:

②可导的充要条件:左导数=右导数=存在
左导数
右导数无穷导数视为不存在
高阶导数:
考点
先看定义法,定义法最多
再想公式抽象f(x)在一点的导数
题目关键词:一点
泛指x
特指
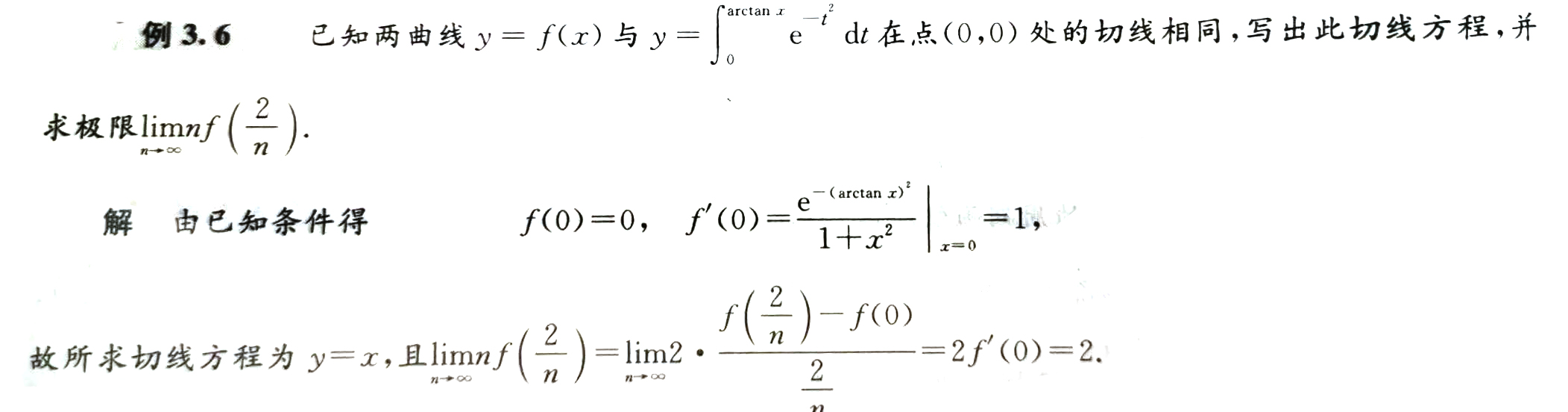
分段函数在分段点
常见绝对值函数

四则运算不方便的
太复杂的点
f = f 1 + f 2 f=f_1+f_2 
f = f 1 f 2 ⋯ f n f=f_1f_2\cdots f_n 
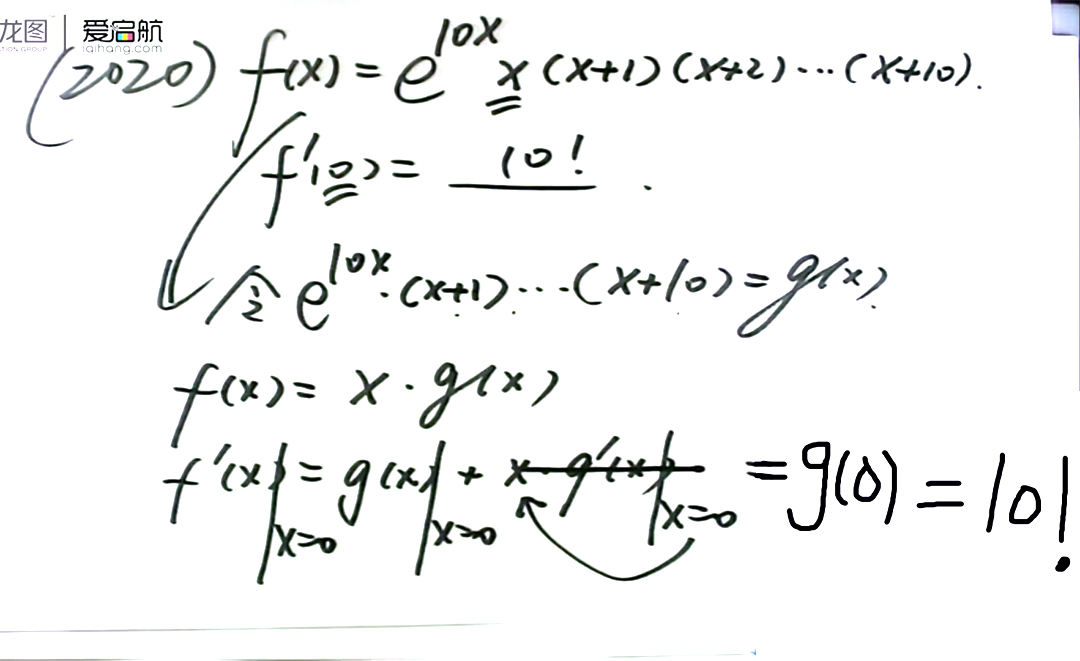
不成立的点
可微概念:
Δ y = A Δ x + o ( Δ x ) , A 与 Δ x 无 关 , o ( Δ x ) 是 Δ x → 0 时 的 高 阶 无 穷 小 \Delta y = A \Delta x+o(\Delta x),A与\Delta x 无关,o(\Delta x)是\Delta x\rightarrow 0时的高阶无穷小 微分记为
d y ∣ x = x 0 = d f ( x ) ∣ x = x 0 = A Δ x = A d x dy|_{x=x_0}=df(x)|_{x=x_0}=A\Delta x=Adx 注意
d x 2 = ( d x ) 2 = d x ⋅ d x dx^2=(dx)^2=dx\cdot dx
d ( x 2 ) = 2 x ⋅ d x d(x^2)=2x\cdot dx
d 2 y d x 2 = d ( d y d x ) d x \frac{d^2y}{dx^2}=\frac{d(\frac{dy}{dx})}{dx}
判别
①
写 增 量 Δ y = f ( x 0 + Δ x ) − f ( x 0 ) 写增量\Delta y = f(x_0+\Delta x)-f(x_0)
②
写 线 性 增 量 A Δ x = f ′ ( x 0 ) Δ x 写线性增量A\Delta x =f'(x_0)\Delta x
③
作 极 限 lim Δ x → 0 Δ y − A Δ x Δ x = ? 0 ⟹ f ( x ) 在 x 0 处 可 微 作极限 {\displaystyle \lim_{\Delta x \rightarrow 0}{\frac{\Delta y-A\Delta x}{\Delta x}} } \stackrel{?}{=}0 \Longrightarrow f(x)在x_0处可微
含义:用简单的
A Δ x A\Delta x Δ y \Delta y
几何意义:
若 f ( x ) 在 点 x 0 处 可 微 , 则 在 点 ( x 0 , y 0 ) 附 近 可 以 用 切 线 段 近 似 替 代 曲 线 段 若f(x)在点x_0处可微,则在点(x_0,y_0)附近可以用切线段近似替代曲线段
仅对一元函数:
x 0 x_0
运算
四则
和差
[ u ( x ) ± v ( x ) ] ′ = u ′ ( x ) ± v ′ ( x ) [u(x)\pm v(x)]'=u'(x)\pm v'(x)
d [ u ( x ) ± v ( x ) ] = d u ( x ) ± d v ( x ) d[u(x)\pm v(x)]=du(x)\pm dv(x)
积
[ u ( x ) v ( x ) ] ′ = 前 导 后 + 后 导 前 = u ′ ( x ) v ( x ) + u ( x ) v ′ ( x ) [u(x)v(x)]'=前导后+后导前=u'(x)v(x)+u(x)v'(x)
d [ u ( x ) v ( x ) ] = d u ( x ) v ( x ) + u ( x ) d v ( x ) d[u(x)v(x)]=du(x)v(x)+u(x)dv(x)
[ u ( x ) v ( x ) w ( x ) ] ′ = u ′ ( x ) v ( x ) w ( x ) + u ( x ) v ′ ( x ) w ( x ) + u ( x ) v ( x ) w ′ ( x ) [u(x)v(x)w(x)]'=u'(x)v(x)w(x)+u(x)v'(x)w(x)+u(x)v(x)w'(x) 遇到因式超过三个的一般不要直接求导,用其他方法
商
[ u ( x ) v ( x ) ] ′ = u ′ ( x ) v ( x ) − u ( x ) v ′ ( x ) [ v ( x ) ] 2 [\frac{u(x)}{v(x)}]'=\frac{u'(x)v(x)-u(x)v'(x)}{[v^(x)]^2} = 子 导 母 − 母 导 子 母 方 =\frac{子导母-母导子}{母方}
逆向应用
f ′ ( x ) + f ( x ) ⟵ g ( x ) = e x f ( x ) g ′ ( x ) = e x [ f ′ ( x ) + f ( x ) ] f'(x)+f(x) \longleftarrow g(x)=e^xf(x) g'(x)=e^x[f'(x)+f(x)]
f ′ ( x ) − f ( x ) ⟵ g ( x ) = e − x f ( x ) g ′ ( x ) = e − x [ f ′ ( x ) − f ( x ) ] f'(x)-f(x) \longleftarrow g(x)=e^{-x}f(x) g'(x)=e^{-x}[f'(x)-f(x)]
x f ′ ( x ) + f ( x ) ⟵ g ( x ) = x f ( x ) g ′ ( x ) = x f ′ ( x ) + f ( x ) xf'(x)+f(x) \longleftarrow g(x)=xf(x) g'(x)=xf'(x)+f(x)
x f ′ ( x ) − f ( x ) ⟵ g ( x ) = x − 1 f ( x ) g ′ ( x ) = x − 2 [ x f ′ ( x ) − f ( x ) ] xf'(x)-f(x) \longleftarrow g(x)=x^{-1}f(x) g'(x)=x^{-2}[xf'(x)-f(x)]
复合
{ f [ g ( x ) ] } ′ = f ′ [ g ( x ) ] g ′ ( x ) \{f[g(x)]\}'=f'[g(x)]g'(x) 微 分 形 式 的 不 变 性 d y = f ′ ( u ) d u 微分形式的不变性dy=f'(u)du
d { f [ g ( x ) ] } = f ′ [ g ( x ) ] g ′ ( x ) d x d\{f[g(x)]\}=f'[g(x)]g'(x)dx 注意看清楚符号的位置
{ f [ g ( x ) ] } ′ = d f [ g ( x ) ] d x \{f[g(x)]\}'=\frac{d{f[g(x)]}}{dx}
f ′ [ g ( x ) ] = d { f [ g ( x ) ] } d g ( x ) f'[g(x)]=\frac{d\{f[g(x)]\}}{dg(x)}
内可导和外可导只是复合函数可导的充分条件,不是必要条件
反函数
一阶
y = f ( x ) 与 x = φ ( y ) 互 为 反 函 数 y=f(x)与x= φ (y)互为反函数
y x ′ = y'_x= d x d y = 1 d y d x \frac{dx}{dy}=\frac{1}{\frac{dy}{dx}}
二阶
y x x ′ ′ = d 2 y d x = d ( d y d x ) d x = d ( 1 x y ′ ) d x = d ( 1 x y ′ ) d y ⋅ 1 x y ′ = − x y y ′ ′ ( x y ′ ) 3 y''_{xx}=\frac{d^2y}{dx}=\frac{d(\frac{dy}{dx})}{dx}=\frac{d(\frac{1}{x'_y})}{dx}=\frac{d(\frac{1}{x'_y})}{dy}\cdot\frac{1}{x'_y}=\frac{-x''_{yy}}{(x'_y)^3}
参数方程
一阶
y=y(x)=\begin{cases} y= α (t)\\ x= β (t) \end{cases}
y x ′ = y'_x= d y d x = d y / d t d x / d t = α ′ ( t ) β ′ ( t ) \frac{dy}{dx}=\frac{dy/dt}{dx/dt}=\frac{ α '(t)}{ β '(t)}
若 α ( t ) , β ( t ) 不 可 导 , 则 用 导 数 定 义 处 理 若 α (t),\beta(t)不可导,则用导数定义处理
二阶
y x x ′ ′ = d 2 y d x 2 = d ( d y d x ) d x = d ( d y d x ) / d t d x / d t = α ′ ′ ( t ) β ′ ( t ) − α ′ ( t ) β ′ ′ ( t ) [ β ′ ( t ) ] 3 y''_{xx}=\frac{d^2y}{dx^2}=\frac{d(\frac{dy}{dx})}{dx}=\frac{d(\frac{dy}{dx})/dt}{dx/dt}=\frac{ α ''(t) β '(t)- α '(t) β ''(t)}{[ β '(t)]^3}
隐函数
y = y ( x ) 是 由 方 程 F ( x , y ) = 0 确 定 的 可 导 函 数 y=y(x)是由方程F(x,y)=0确定的可导函数
方 程 F ( x , y ) = 0 两 边 对 自 变 量 x 求 导 , 注 意 y = y ( x ) , 也 就 是 将 y 看 做 中 间 变 量 , 得 到 一 个 关 于 y ′ 的 方 程 , 解 出 这 个 y ′ 方程F(x,y)=0两边对自变量x求导,注意y=y(x),也就是将y看做中间变量,得到一个关于y'的方程,解出这个y'
对数
对于多项相乘、相除、开放、乘方的式子,先取对数再求导
① y = f ( x ) ⟹ ln y = ln f ( x ) ①y=f(x)\Longrightarrow \ln y=\ln f(x)
② ( ln y ) ′ = ( ln f ( x ) ) ′ ⟹ 1 y y ′ = [ ln f ( x ) ] ⟹ y ′ = y [ ln f ( x ) ] ′ ② (\ln y)'=(\ln f(x))'\Longrightarrow \frac{1}{y}y'=[\ln f(x)]\Longrightarrow y'=y[\ln f(x)]'
注意仍然把y看成中间变量
幂指
对 于 u ( x ) v ( x ) , 除 了 导 数 法 , 还 可 以 转 换 幂 指 再 求 导 对于u(x)^{v(x)},除了导数法,还可以转换幂指再求导 ① u ( x ) v ( x ) = e v ( x ) ln u ( x ) ①u(x)^{v(x)}=e^{v(x)\ln u(x)}
[ u ( x ) v ( x ) ] ′ = [ e v ( x ) ln u ( x ) ] ′ = u ( x ) v ( x ) [ v ′ ( x ) ⋅ ln u ( x ) + v ( x ) ⋅ u ′ ( x ) u ( x ) ] [u(x)^{v(x)}]'=[e^{v(x)\ln u(x)}]'=u(x)^{v(x)}[v'(x)\cdot\ln u(x)+v(x)\cdot\frac{u'(x)}{u(x)}]
高阶
逐次求导,寻找规律
注意适当化简因式分解
( sin k x ) ( n ) = k n sin ( k x + n ⋅ π 2 ) (\sin k x)^{(n)}=k^n \sin (kx+n\cdot \frac{ π }{2}) ( cos k x ) ( n ) = k n cos ( k x + n ⋅ π 2 ) (\cos k x)^{(n)}=k^n \cos (kx+n\cdot \frac{ π }{2})
( a x ) ( n ) = a x ( ln a ) n (a^x)^{(n)}=a^x(\ln a)^n
( e x ) ( n ) = e x (e^x)^{(n)}=e^x
( ln x ) ( n ) = ( − 1 ) n − 1 ( n − 1 ) ! x n (\ln x)^{(n)}=(-1)^{n-1}\frac{(n-1)!}{x^n}
[ ln ( 1 + x ) ] ( n ) = ( − 1 ) n − 1 ( n − 1 ) ! ( 1 + x ) n [\ln (1+x)]^{(n)}=(-1)^{n-1}\frac{(n-1)!}{(1+x)^n}
[ ( x + x 0 ) m ] ( n ) = m ( m − 1 ) ( m − 2 ) ⋯ ( m − n + 1 ) ( x + x 0 ) m − n [(x+x_0)^m]^{(n)}=m(m-1)(m-2)\cdots(m-n+1)(x+x_0)^{m-n}
( 1 x + a ) ( n ) = ( − 1 ) n n ! ( x + a ) n + 1 (\frac{1}{x+a})^{(n)}=\frac{(-1)^nn!}{(x+a)^{n+1}}
高阶求导公式
[ u ± v ] ( n ) = u ( n ) ± v ( n ) [u\pm v]^{(n)}=u^{(n)}\pm v^{(n)}
莱布尼兹公式:
( u v ) ( n ) = u ( n ) v + C n 1 u ( n − 1 ) v ′ + ⋯ + C n k u ( n − k ) v ( k ) + ⋯ + u v ( n ) (uv)^{(n)}=u^{(n)}v+C_n^1u^{(n-1)}v'+\cdots+C_n^ku^{(n-k)}v^{(k)}+\cdots+uv^{(n)} ( u v ) ( 3 ) = u ( 3 ) v + 3 u ( 2 ) v ′ + 3 u ′ v ( 2 ) + u v ( 3 ) (uv)^{(3)}=u^{(3)}v+3u^{(2)}v'+3u'v^{(2)}+uv^{(3)}
( u v ) ( 4 ) = u ( 4 ) v + 4 u ( 3 ) v ′ + 6 u ′ ′ v ′ ′ + 4 u ′ v ( 3 ) + u v ( 4 ) (uv)^{(4)}=u^{(4)}v+4u^{(3)}v'+6u''v''+4u'v^{(3)}+uv^{(4)}
与泰勒展开式比较系数
1-任何一个无穷可导的函数都可以写成
y = f ( x ) = ∑ n = 0 ∞ f ( n ) ( x 0 ) n ! ( x − x 0 ) n y=f(x)= {\displaystyle \sum_{n=0}^{\infty}{\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n} }
2-写出f(x)的泰勒展开式
3-比较相同幂次的系数,根据函数展开式的唯一性,两个系数相同
变限积分
F ( x ) = ∫ φ 1 ( x ) φ 2 ( x ) f ( t ) d t F(x)= \int_ {φ _1(x)}^{φ _2(x)}f(t)dt
F ′ ( x ) = d d x [ ∫ φ 1 ( x ) φ 2 ( x ) f ( t ) d t ] = f [ φ 2 ( x ) ] φ 2 ′ ( x ) − f [ φ 1 ( x ) ] φ 1 ′ ( x ) F'(x)= \frac{d}{dx}[\int_ {φ _1(x)}^{φ _2(x)}f(t)dt ]=f[φ _2(x)]φ' _2(x)-f[φ _1(x)]φ' _1(x)
基本初等函数的导数
( x α ) ′ = α x α − 1 (x^ α )'= α x^{ α -1}
( a x ) ′ = a x ln a (a^x)'=a^x\ln a
( e x ) ′ = e x (e^x)'=e^x
( log a x ) ′ = 1 x ln a (\log_a x)'=\frac{1}{x\ln a}
( ln x ) ′ = 1 x (\ln x)'=\frac{1}{x}
( ln ∣ x ∣ ) ′ = 1 x (\ln |x|)'=\frac{1}{x}
( sin x ) ′ = cos x (\sin x)'=\cos x
( cos x ) ′ = − sin x (\cos x)'=-\sin x
( tan x ) ′ = sec 2 x (\tan x)'=\sec^2x
( cot x ) ′ = − csc 2 x (\cot x)'=-\csc^2x
( sec x ) ′ = sec x tan x (\sec x)'=\sec x \tan x
( csc x ) ′ = − csc x cot x (\csc x)'=-\csc x \cot x
( ln ∣ cos x ∣ ) ′ = − t a n x (\ln |\cos x|)'=-tan x
( arcsin x ) ′ = 1 1 − x 2 (\arcsin x)'=\frac{1}{\sqrt{1-x^2}}
( arccos x ) ′ = − 1 1 − x 2 (\arccos x)'=-\frac{1}{\sqrt{1-x^2}}
( arctan x ) ′ = 1 1 + x 2 (\arctan x)'=\frac{1}{1+x^2}
( arccot x ) ′ = − 1 1 + x 2 (\textrm{arccot}x)'=-\frac{1}{1+x^2}
[ ln ( x + x 2 + a 2 ) ] ′ = 1 x 2 + a 2 [\ln (x+\sqrt{x^2+a^2})]'=\frac{1}{\sqrt{x^2+a^2}}
[ ln ( x + x 2 − a 2 ) ] ′ = 1 x 2 − a 2 [\ln (x+\sqrt{x^2-a^2})]'=\frac{1}{\sqrt{x^2-a^2}} x>a
几何应用
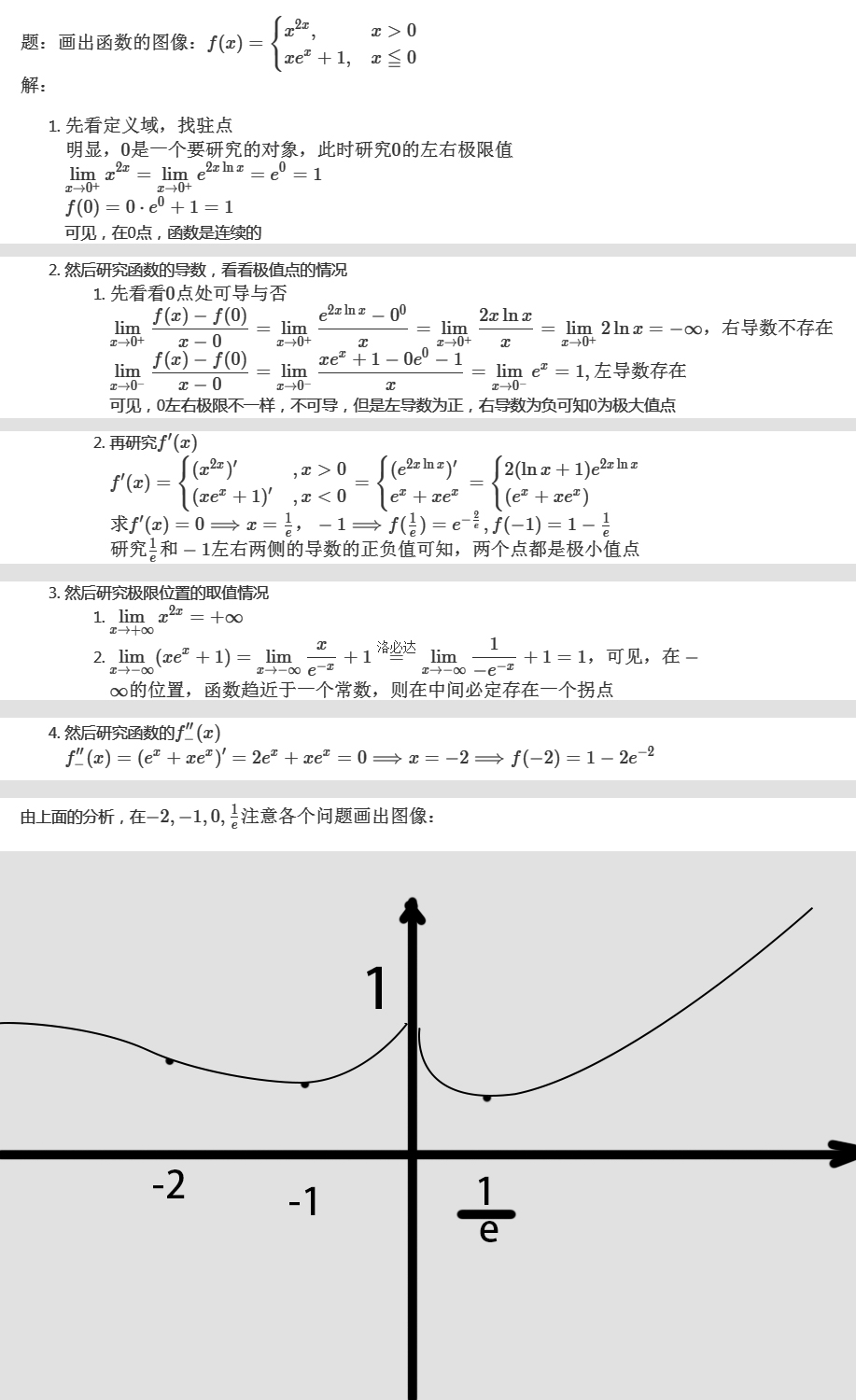
作函数图像
①确定定义域
②奇偶性、对称性
③求
f ′ ( x ) 和 f ′ ′ ( x ) f'(x)和f''(x)
f ( x ) f(x)
f ′ ( x ) = 0 f'(x)=0
f ′ ( x ) 不 存 在 的 点 f'(x)不存在的点
f ′ ′ ( x ) = 0 的 点 f''(x)=0的点
f ′ ′ ( x ) 不 存 在 的 点 f''(x)不存在的点
④把以上点将定义域划分区域段,判断区域段内的单调性和凹凸性
确定极值点和拐点
⑤确定渐进线
⑥作图
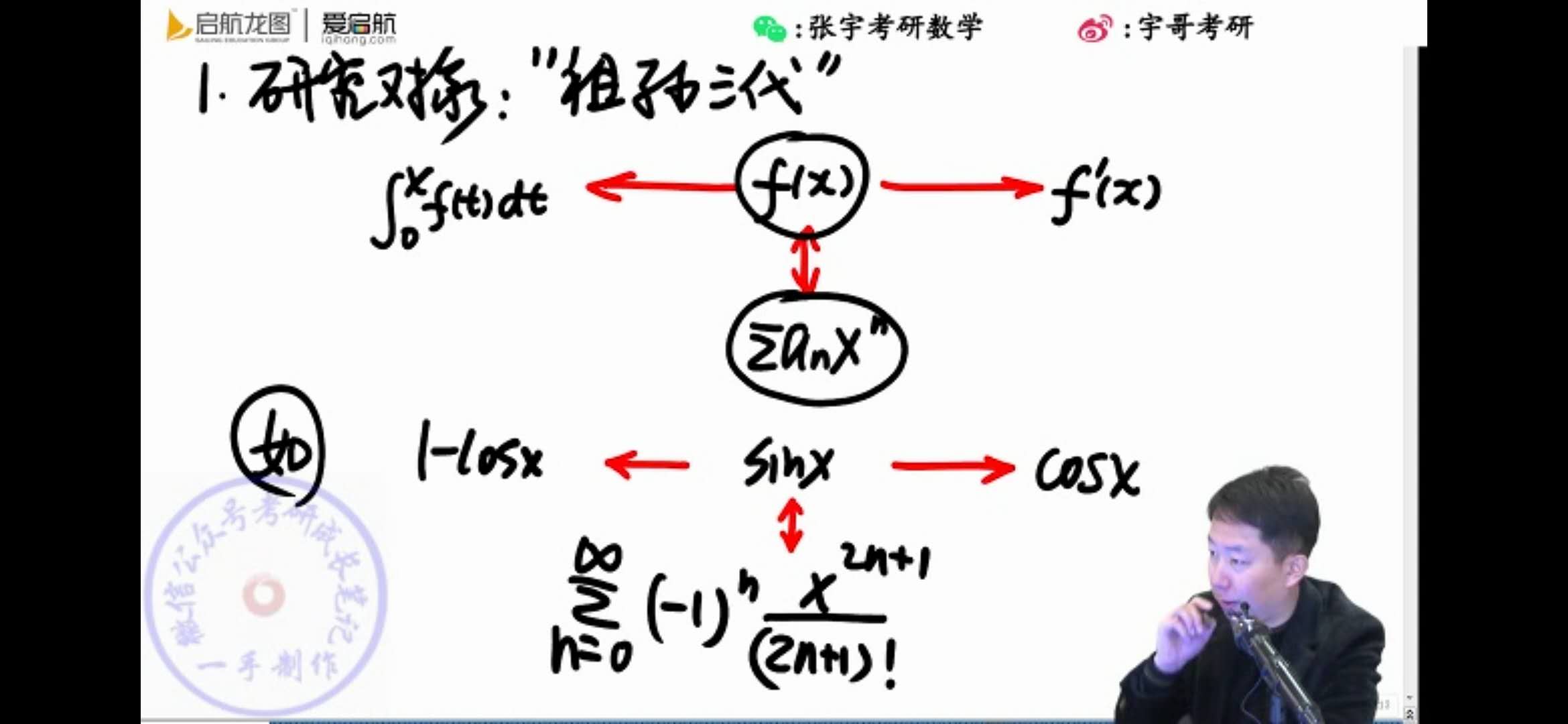
研究对象与内容
研究对象
祖孙三代
函 数 f ( x ) , 函 数 簇 f n ( x ) , 简 单 函 数 四 则 运 算 f 1 ( x ) f 2 ( x ) ⋯ f n ( x ) 函数f(x),函数簇f_n(x),简单函数四则运算f_1(x)f_2(x)\cdots f_n(x)
f ′ ( x ) , 、 d f ( x ) d x 2 = 1 2 x f ′ ( x ) f'(x),、\frac{df(x)}{dx^2}=\frac{1}{2x}f'(x)
∫ a x f ( t ) d t \int_a^xf(t)dt
∑ a n x n {\displaystyle \sum_{}^{}{a_nx^n} }
分段函数(含绝对值函数,符号sgn函数,取整函数)
参数方程
{ x = x ( t ) y = y ( t ) \begin{cases} x=x(t)\\ y=y(t) \end{cases} r = r ( θ ) = { x = r cos θ = r ( θ ) cos θ = x ( θ ) y = r sin θ = r ( θ ) sin θ = y ( θ ) r=r( θ ) =\begin{cases} x=r\cos θ=r( θ )\cos θ =x (θ) \\ y=r\sin θ=r( θ ) \sin θ =y( θ ) \end{cases} 一阶
y ′ ( x ) = d y d x = d y / d t d x / d t = y ′ ( t ) x ′ ( t ) = f ( t ) y'(x)=\frac{dy}{dx}=\frac{dy/dt}{dx/dt}=\frac{y'(t)}{x'(t)}=f(t)
二阶
y ′ ′ ( x ) = d 2 y d x 2 = d ( d y d x ) d x = d ( f ( t ) ) / d t d x / d t y''(x)=\frac{d^2y}{dx^2}=\frac{d(\frac{dy}{dx})}{dx}=\frac{d(f(t))/dt}{dx/dt}
隐函数F(x,y)=0
研究内容
三点两性一线斜率
y = y ( x ) ⟹ y ′ ( x 0 ) = k y=y(x)\Longrightarrow y'(x_0)=k 切 线 方 程 : y − y 0 = f ′ ( x 0 ) ( x − x 0 ) 切线方程:y-y_0 = f'(x_0)(x-x_0)
法 线 方 程 : y − y 0 = − 1 f ′ ( x 0 ) ( x − x 0 ) ( f ′ ( x 0 ) ̸ = 0 ) 法线方程:y-y_0 = -\frac{1}{f'(x_0)}(x-x_0)(f'(x_0) \ne 0)
单调性和极值点
单调性
f ′ ( x ) > 0 ⟹ 单 增 , f ′ ( x ) < 0 ⟹ 单 减 f'(x)>0 \Longrightarrow 单增,f'(x)<0 \Longrightarrow 单减
极值与最值
f ( x 0 ) f(x_0)
极值点与最值点x 0 x_0 极值
广义:若存在
x 0 x_0 f ( x ) ≦ f ( x 0 ) f(x)\leqq f(x_0) x 0 x_0 f ( x ) f(x)
真:若存在
x 0 x_0 x 0 x_0 f ( x ) ≦ f ( x 0 ) f(x)\leqq f(x_0) x 0 x_0 f ( x ) f(x)
最值
广义:
x 0 x_0 f ( x ) ≦ f ( x 0 ) f(x)\leqq f(x_0) x 0 x_0 f ( x ) f(x)
真:
x 0 x_0 x 0 x_0 f ( x ) ≦ f ( x 0 ) f(x)\leqq f(x_0) x 0 x_0 f ( x ) f(x)
关系
极值点不一定是最值点,最值点也不一定是极值点
如果
f ( x ) f(x) I I x 0 x_0 x 0 x_0 I I f ( x ) f(x)
定理
必要条件
x 0 是 极 值 点 ⟹ f ′ ( x 0 ) = 0 x_0是极值点\Longrightarrow f'(x_0)=0
x 0 称 为 驻 点 x_0称为驻点 求出来驻点,只能作为待定,运用充分条件再去判断
第一充分条件
f ( x ) 在 x 0 处 连 续 , 在 去 心 邻 域 U ˚ ( x 0 , δ ) 内 可 导 , f ′ ( x ) 在 x 0 左 右 符 号 不 同 ⟹ 极 值 f(x)在x_0处连续,在去心邻域\mathring{U}(x_0, δ )内可导,f'(x)在x_0左右符号不同\Longrightarrow 极值
第二充分条件
f ( x ) 在 x 0 处 二 阶 可 导 , f ′ ( x 0 ) = 0 , f ′ ′ ( x 0 ) ̸ = 0 f(x)在x_0处二阶可导,f'(x_0)=0,f''(x_0)\neq 0
f ′ ′ ( x 0 ) < 0 ⟹ 极 大 值 , f ′ ′ ( x 0 ) > 0 ⟹ 极 小 值 f''(x_0)<0 \Longrightarrow 极大值,f''(x_0)>0 \Longrightarrow 极小值
第三充分条件
f ( x ) 在 x 0 处 n 阶 可 导 , f ( m ) ( x 0 ) = 0 ( m = 1 , 2 , ⋯ , n − 1 ) , f ( n ) ( x 0 ) ̸ = 0 ( n ≧ 2 ) f(x)在x_0处n阶可导,f^{(m)}(x_0)=0(m=1,2,\cdots,n-1),f^{(n)}(x_0)\neq 0(n\geqq2) n为偶数
⟹ \Longrightarrow
f ( n ) ( x 0 ) < 0 ⟹ 极 大 , f ( n ) ( x 0 ) > 0 ⟹ 极 小 f^{(n)}(x_0)<0\Longrightarrow 极大,f^{(n)}(x_0)>0\Longrightarrow 极小
导数法求函数最值:①求导数 ②求根(因式分解) ③穿根(奇穿偶不穿) ④作图
凹凸性与拐点
充分条件
f ′ ′ ( x ) > 0 ⟹ 凹 , f ′ ′ ( x ) < 0 ⟹ 凸 f''(x)>0\Longrightarrow 凹,f''(x)<0\Longrightarrow 凸
f ( x 1 ) + f ( x 2 ) 2 > f ( x 1 + x 2 2 ) ⟹ 凹 \frac{f(x_1)+f(x_2)}{2}>f(\frac{x_1+x_2}{2})\Longrightarrow 凹 f ( x 1 ) + f ( x 2 ) 2 < f ( x 1 + x 2 2 ) ⟹ 凸 \frac{f(x_1)+f(x_2)}{2}<f(\frac{x_1+x_2}{2})\Longrightarrow 凸
拐点
( x 0 , f ( x 0 ) ) (x_0,f(x_0)) 必要条件
x 0 为 拐 点 ⟹ f ′ ′ ( x 0 ) = 0 x_0为拐点\Longrightarrow f''(x_0)=0
第一充分条件
f ′ ′ ( x ) 在 x 0 左 右 变 号 ⟹ x 0 拐 点 f''(x)在x_0左右变号\Longrightarrow x_0拐点 并不要求
f ( x ) f(x) x 0 x_0
第二充分条件
三 阶 可 导 , f ′ ′ ( x 0 ) = 0 , f ′ ′ ′ ( x 0 ) ̸ = 0 ⟹ 拐 点 三阶可导,f''(x_0)=0,f'''(x_0)\neq0\Longrightarrow 拐点
第三充分条件
f ( x ) 在 x 0 处 n 阶 可 导 , f ( m ) ( x 0 ) = 0 ( m = 1 , 2 , ⋯ , n − 1 ) , f ( n ) ( x 0 ) ̸ = 0 ( n ≧ 2 ) f(x)在x_0处n阶可导,f^{(m)}(x_0)=0(m=1,2,\cdots,n-1),f^{(n)}(x_0)\neq 0(n\geqq2) n为奇数
⟹ \Longrightarrow
x 0 为 拐 点 x_0为拐点 不需要
f ′ ( x 0 ) = 0 f'(x_0)=0
渐近线
水平
若 lim x → + ∞ f ( x ) = lim x → − ∞ f ( x ) = y 0 , 则 y = y 0 为 一 条 水 平 渐 近 线 若\displaystyle{\lim_{x\to+\infty}f(x)=\lim_{x\to-\infty}f(x)}=y_0,则y=y_0为一条水平渐近线 看
± ∞ \pm \infty
铅直
若 lim x → x 0 + f ( x ) = ∞ ( 或 x → x 0 − ) , 则 x = x 0 为 一 条 铅 直 渐 近 线 若\displaystyle{\lim_{x\to x^+_0}f(x)}=\infty (或x \to x_0^-),则x=x_0为一条铅直渐近线 找无定义点或者端点
斜
若①
lim x → + ∞ f ( x ) x = lim x → − ∞ f ( x ) x = k \displaystyle{\lim_{x\to +\infty}\frac{f(x)}{x}=\lim_{x\to -\infty}\frac{f(x)}{x}}=k ̸ = 0 \neq 0 lim x → + ∞ [ f ( x ) − k x ] = lim x → − ∞ [ f ( x ) − k x ] = b \displaystyle{\lim_{x\to +\infty}[f(x)-kx]=\lim_{x\to -\infty}[f(x)-kx]}=b 注意看x是一次的,所以上面的f(x)也必须是x的同阶的
值域最值点
闭区间[a,b]内
①驻点和不可导点的函数值
②端点的函数值f(a)和f(b)
③比较以上各值
开区间(a,b)内
①驻点和不可导点的函数值
②求端点的单侧极限
lim x → a + f ( x ) 和 lim x → b − f ( x ) \displaystyle{\lim_{x\to a^+}f(x)}和\displaystyle{\lim_{x\to b^-}f(x)}
③比较以上各值
高阶导数
研究对象和研究内容任意组合
函数簇
f n ( x ) f_n(x) 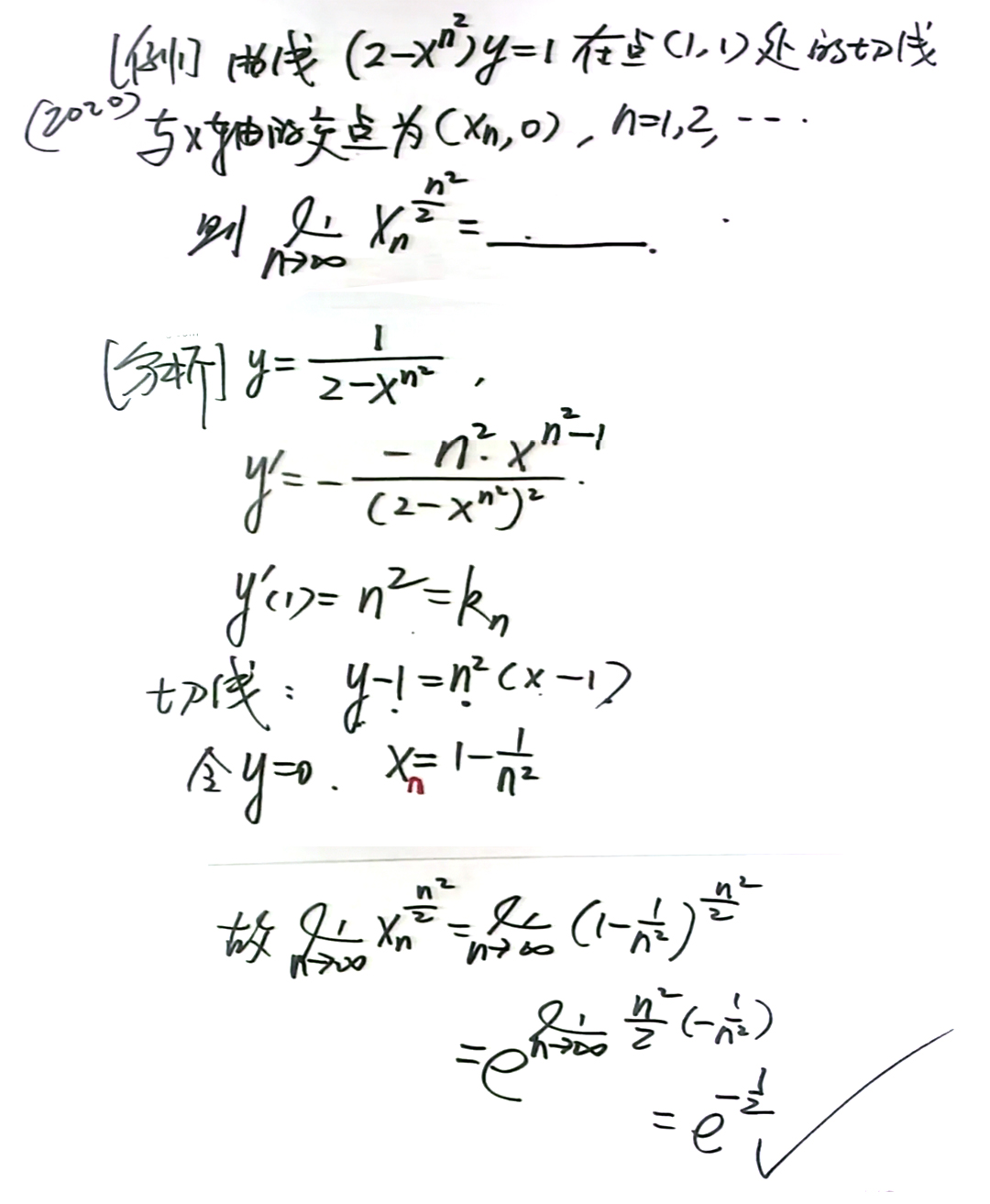
和函数
∑ a n x n {\displaystyle \sum_{}^{}{a_nx^n} } 
参数方程+凹凸性、拐点

复杂
f ( x ) f(x) 
隐函数+极值

综合