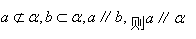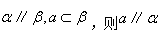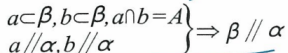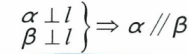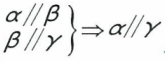空间的平行关系

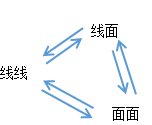
• ​线线平行

  • ​判定

    • ​定义：空间两条直线共面，且没有公共点

    • ​平行的传递性：空间两直线垂直于第三条直线，则这两条直线平行

      • 

    • ​线面平行的性质定理：直线平行平面，则直线与过该直线和已知平面的交线平行

      • 

      • 

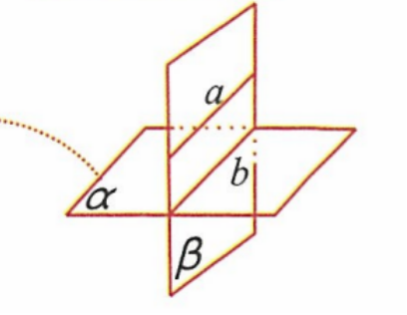
    • ​面面平行的性质定理：一个平面与已知两平行平面相交，则交线平行

      • 

      • 

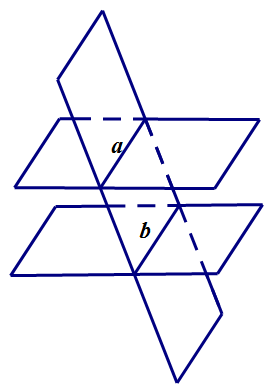
    • ​线面垂直的性质定理：同垂直于一个平面的两直线平行

      • 

      • 

    • ​平面几何中的判定方法

• ​核心素养：逻辑推理，直观想象，数学建模

• ​线面平行

  • ​定义：直线与平面没有交点

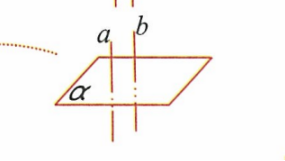
  • ​线面平行的判定定理：平面外一条直线与平面内一条直线平行，则直线与平面平行

    • 

    • 

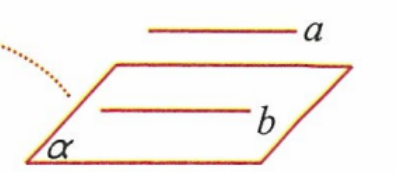
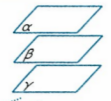
  • ​面面平行的定义：两平面平行，则其中一个平面内的任意一条直线会平行于第二个平面

    • 

  • ​结论：一条直线与一个平面都与第二个平面平行，若直线不在第一个平面内，则直线与第一个平面平行

    • 

      ​

    • 

• 

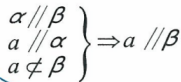
  ​数学思想方法：转化与化归，

• ​面面平行

  • ​定义：两个平面没有公共点

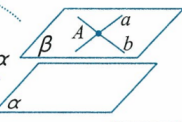
  • ​判定定理：一个平面内有两条相交线都平行于第二个平面，则这两个平面平行

    • 

    • 

  • ​线面垂直的推论：空间两平面都垂直于一条直线，则这两个平面平行

    • 

    • 

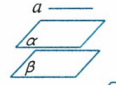
  • ​平行的传递性：两个平面都平行于第三个平面，则这两个平面平行

    • 

    •